Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

Современная квантовая химия берет начало с работы немецких ученых Вальтера Гайтлера и Фрица Лондона "Взаимодействие нейтральных атомов и гомеополярная связь с точки зрения квантовой механики", опубликованной в 1927 г. [50].

Используя математический аппарат квантовой механики, Гайтлер и Лондон решили задачу об изменении энергии двух электронейтральных атомов водорода, находящихся в основном состоянии, когда их ядра сближаются до конечного расстояния R. Задача решалась в терминах квантовомеханической теории возмущений, использованной незадолго до этого Вернером Гейзенбергом при анализе состояний двухэлектронной системы атома Не. Исследование Гейзенберга в известной мере подготовило почву для создания теории гомеополярной (ковалентной) химической связи, однако, как будет показано дальше, между его подходом и методом Гайтлера-Лондона имеются некоторые различия.

Гайтлер и Лондон аппроксимировали двухэлектронную функцию, описывающую электронное состояние молекулы Н 2, произведением одноэлектронных функций (орбиталей) а( r) и b( r) изолированных атомов водорода, центрированных на конечном расстоянии друг от друга. Разумеется, обе функции имеют при этом одинаковый вид:

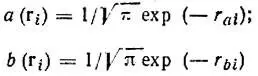(3.1)

и отвечают локализации i-го электрона соответственно около ядра A и В.

Однако, как замечают авторы, их выводы остаются в силе, если а( r) и b( r) "различны и по своей структуре, так что приведенное рассмотрение распространяется на значительно более общий случай" [50, с. 457], т. е. на другие молекулы.

В качестве невозмущенных собственных функций Гайтлер и Лондон выбрали такие, которые соответствуют локализации одного электрона у ядра А, а другого — у ядра В. Если несвязанные атомы А и В рассматривать как единую систему, то произведение соответствующих им собственных функций представляет собой собственную функцию этой системы, причем можно построить две двухэлектронные функции вида: а( r 1 )*b( r 2 ) (первый электрон около ядра A, второй — около ядра В); a( r 2 )b( r 1 ) (первый электрон около ядра В, второй — около ядра А).

Обе возможности соответствуют одной и той же энергии системы (удвоенной энергии атома водорода) — случай двукратного вырождения. Любые две линейные комбинации

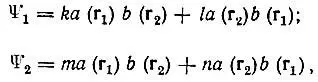(3.2)

удовлетворяющие условиям нормировки и ортогональности:

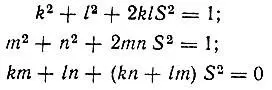(3.3)

[где 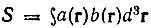— интеграл перекрывания атомных орбиталей а( r) и b( r)] следует рассматривать как невозмущенные собственные функции двухэлектронной задачи. Коэффициенты k, l, m, n можно определить из одних только условий симметрии. При этом оптимальные функции нулевого приближения теории возмущений для рассматриваемого существенно вырожденного случая будут иметь вид:

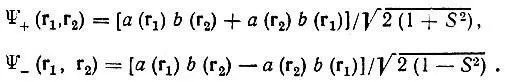(3.4)

Очевидно, что функции 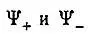нормированны и ортогональны.

Применив стандартную теорию возмущений, Гайтлер и Лондон нашли, что поправки к энергии нулевого приближения, соответствующие функциям 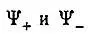, определяются формулами:

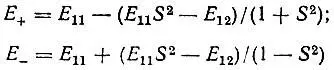(3.5)

или в объединенной форме:

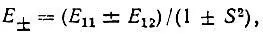(3.6)

где

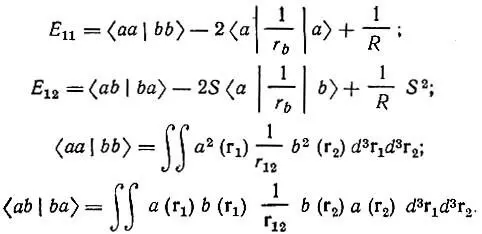
Наиболее интересным с химической точки зрения является второй параграф работы Гайтлера и Лондона, посвященный анализу формул. Прежде всего авторы указывают на трудность физической интерпретации полученного в предыдущем параграфе результата, согласно которому "два нейтральных атома могут взаимодействовать двумя различными способами... От истинного понимания этого обстоятельства мы еще, вероятно, далеки. Но желательно выяснить, по крайней мере с математической точки зрения, причину появления этой замечательной двойственности (zweideutigkeit) " [50, с. 458].

С этой целью Гайтлер и Лондон используют следующие рассуждения. При бесконечном удалении ядер 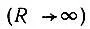энергия системы двукратно вырождена соответственно двум возможным распределениям неразличимых электронов по электронейтральным атомам водорода. "В то время как в классической механике существует возможность четко различать электроны, "наклеить этикетку" (электрон для этого необходимо поместить в достаточно глубокую потенциальную яму и изолировать от всякого доступа энергии), что-либо подобное в квантовой механике невозможно. Если в некоторый момент времени известно, что один электрон находится в потенциальной яме, никогда нельзя быть уверенным, что уже в следующий момент он не обменяется с другим электроном" [50, с. 460].

При сближении атомов упомянутое выше двукратное вырождение снимается и сходный энергетический уровень Е 0расщепляется на два 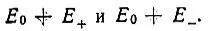Чтобы выяснить относительное расположение этих уровней, авторы обратились к теории Штурма-Лиувилля, согласно которой безузловой собственной функции соответствует наименьшее собственное значение.