Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

Три ортогональных оси координат необходимы для указания положения объекта в пространстве. Если же речь идет об определении направления (а именно это и требовалось для правильной ориентации космического корабля перед включением тормозных двигателей), то достаточно осуществить поворот по двум осям. Именно столько их у телескопа и артиллерийского орудия.

Однако в аэродинамике летательных аппаратов (самолетов), откуда терминология перекочевала в космонавтику, направление летящего самолета описывается тремя углами: крен, тангаж и рыскание. Крен изменяется при покачивании крыльями, тангаж — при покачивании с носа на корму, а рыскание — это повороты вправо-влево. Дело в том, что при полете в атмосфере важна ориентация плоскости крыльев, создающих подъемную силу, относительно направления силы тяжести, которую эта сила должна компенсировать.

У космического корабля нет крыльев, а если и есть (ракетоплан), то в вакууме они не создают подъемной силы. Поэтому крен для корабля на орбите, вообще говоря, безразличен. Но он важен для работы космонавта. Правильный выбор крена позволяет ему увидеть в иллюминатор или перископ поверхность Земли, видимое движение которой указывает направление полета корабля. Именно в этом направлении должна быть сориентирована продольная ось корабля, чтобы работа тормозных двигателей привела к сходу с орбиты и посадке на Землю. Так что в описании полета Джона Гленна неточности не было.

Автоматические межпланетные зонды для ориентации в пространстве осуществляют развороты по двум осям, используя в качестве опорных направления на Солнце и какую-нибудь яркую звезду, например Канопус или Сириус. При этом информацию о направлении своего движения сам зонд получить не может, и ее определяют на Земле путем небесно-механических расчетов.

Формально, двигаясь с постоянной начальной скоростью, снаряд преодолел бы это расстояние за 3,5 года. Однако, учитывая, что вторая космическая скорость на поверхности Солнца 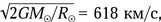а скорость снаряда 1,5 км/с, ясно, что снаряд вообще не покинет Солнце.

Чтобы улететь далеко-далеко, нужно развить вторую космическую скорость:

где M и R — масса и радиус космического тела. Чтобы облегчить расчеты, преобразуем эту формулу. Для сферического тела

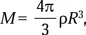
где ρ — средняя плотность тела. Используя значение второй космической скорости для Земли (11,2 км/с), запишем

где R ⊕= 6371 км и ρ ⊕= 5,52 г/см 3— радиус и средняя плотность Земли. Примем плотность типичного астероида равной 2 г/см 3и получим простую формулу для второй космической скорости:

V ∞= 1 м/с × R (км).

То есть вторая космическая скорость, выраженная в метрах в секунду, равна радиусу астероида, выраженному в километрах. Если у тела иная средняя плотность, следует умножить значение V ∞на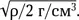

А теперь вопрос посложнее: какую вертикальную скорость может развить человек в прыжке? Подпрыгивая вверх на Земле, мы в основном тратим запас мышечной энергии на преодоление силы тяжести, а на астероиде — на сообщение телу кинетической энергии. Поэтому запишем уравнение так:

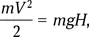
где V — максимальная скорость нашего прыжка на астероиде, m — масса тела человека (она сокращается), g — ускорение свободного падения на Земле, H — максимальное вертикальное перемещение человека в прыжке на Земле. Присев и подпрыгнув, мы перемещаем свое тело примерно на 1 м. Следовательно, 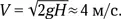Трудно сказать, насколько скафандр затрудняет прыжки: ждем подсказки от тех, кто прыгал в скафандре. А пока примем оценку в 4 м/с как максимальную. Тогда максимальный размер астероида, с которого человек может спрыгнуть в космос и улететь далеко-далеко, составит

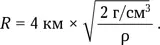
У самых плотных астероидов средняя плотность не превышает 4 г/см 3, а у рыхлых ядер комет она около 0,5 г/см 3, поэтому диапазон значений R составляет от 3 до 8 км. Скорее всего, эти оценки немного завышены. Ведь мы с вами никогда не прыгали в космическом скафандре на астероиде. Может быть, это совсем не легко? Ждем уточнения от тех, кому впервые удастся это сделать.

Солнцем освещена половина лунного шара, поэтому на каждом орбитальном витке спутник будет снимать только половину времени. Если съемка ведется в оптическом диапазоне, то за 14 дней (примерно половина орбитального периода Луны, равного 27,3 сут) спутник снимет только половину лунного шара. Если же это тепловая (ИК) или нейтронная съемка, то можно исследовать весь шар.

Быстрее всего под спутником будут перемещаться экваториальные области Луны. Если орбитальный период аппарата P , то линейное смещение экваториальной области за это время составляет 2π RP /27,3 сут, где R = 1737 км — радиус Луны. Орбитальный период спутника составляет 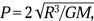где M = 7,35 · 10 22кг — масса Луны. Чтобы не проводить длительных вычислений, воспользуемся знанием того, что период обращения на низкой (около 200 км) околоземной орбите равен 90 мин. Масса Луны — 0,0123 земной массы, радиус Луны — 0,273 земного радиуса, а с учетом высоты орбиты над Луной (100 км) и над Землей (200 км) — 0,280 земного радиуса. Поэтому Тогда ширина полосы составит 2π×1737 км × 2 час / 27,3 сут = 33,3 км. С высоты 100 км эта полоса видна под углом α = 2π arctg (33,3/200) = 18,9°. Таким образом, минимальный угол поля зрения прибора составляет около 19°. Но если это оптический прибор, то съемкой будет покрыта лишь половина Луны.