Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

Самопроизвольное размножение космического мусора происходит по принципу цепной реакции: при столкновении любых двух объектов возникают тысячи новых осколков, поэтому вероятность их последующих столкновений с другими объектами возрастает. До тех пор, пока все осколки не раздробятся до миниатюрного размера, их количество должно было бы возрастать экспоненциально. Однако есть и конкурирующий процесс: осколки на самых низких орбитах интенсивно тормозятся в разреженных слоях земной атмосферы, сгорают в ней или падают на поверхность Земли. Этим объясняется первоначальный спад теоретических кривых (быстро падают фрагменты с самых низких орбит), который затем сменяется ростом числа осколков на более высоких орбитах. Самое тревожное, что даже при полном запрете новых запусков этот рост не прекратится и работать на околоземных орбитах будет все опаснее. Если искусственно не очищать их от мусора. Проектами такой очистки сегодня заняты многие космические инженеры.

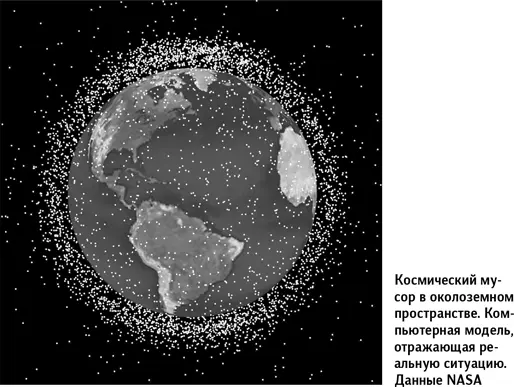
Пилообразная форма кривых связана с «дыханием» земной атмосферы. Синхронно с изменением солнечной активности, происходящим со средним периодом 11,2 года, верхние слои нашей атмосферы «вспухают» и «опадают». В годы повышенной активности Солнца на высотах до 600 км плотность воздуха заметно возрастает, увеличивая сопротивление движению спутников и фрагментов мусора, поэтому они чаще падают на Землю; убыль осколков превышает их размножение. В годы низкой активности Солнца торможение в атмосфере ослабевает и на первый план выходит размножение осколков.

Почти каждый космодром выполняет две функции — военную и гражданскую. Важнейшая военная задача — запуск баллистических ракет в сторону потенциального противника. Все «потенциальные противники» расположены в Северном полушарии, поэтому для минимального подлетного времени требуется полет ракеты через область Северного полюса. Кроме того, для разведывательных и гражданских целей запускают спутники дистанционного наблюдения всей поверхности Земли, которые по определению должны двигаться на полярных орбитах. Действительно, на экваториальной орбите спутник «видит» только область экватора. Чем больше наклон орбиты к экватору, тем шире область наблюдения. На полярной орбите спутник благодаря вращению Земли за 12 часов может «увидеть» всю Землю.

Кроме этого, большие преимущества для наблюдения земной поверхности дает солнечно-синхронная орбита (иногда ее называют гелиосинхронной) — это геоцентрическая орбита с такими параметрами, что объект, находящийся на ней, проходит над любой точкой земной поверхности приблизительно в одно и то же местное солнечное время. Например, наблюдение в утреннее и вечернее время, благодаря длинным теням, позволяет заметить небольшие объекты. Поэтому спутник должен все время двигаться недалеко от линии терминатора, которая всегда проходит недалеко от полюсов (не дальше 23,4°).

Чтобы орбита была гелиосинхронной, ее параметры выбирают такими, чтобы она прецессировала в восточном направлении на 360° в год (приблизительно на 1 градус в день), компенсируя вращение Земли вокруг Солнца. Прецессия происходит за счет взаимодействия спутника с Землей, несферичной из-за полярного сжатия. Скорость прецессии зависит от наклонения орбиты. Нужной скорости прецессии можно достичь лишь для определенного диапазона высот орбит (как правило, выбираются значения 600÷800 км, с периодами 96÷100 минут), необходимое наклонение для упомянутого диапазона высот — около 98°. Иными словами, гелиосинхронная орбита — это практически полярная орбита.

При запуске спутника на полярную орбиту с экваториального космодрома пришлось бы скоростью ракеты компенсировать вращение Земли, которое в данном случае только мешает. Поэтому высокоширотные космодромы в этом случае выгоднее.

Пусть М ⊕— масса Земли и R ⊕— радиус Земли. Полет спутника по низкой орбите от одного полюса к другому займет половину его орбитального периода:

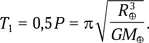
Теперь определим продолжительность полета снаряда через шахту. Поскольку распределение плотности вещества внутри Земли имеет довольно сложный вид, мы рассмотрим два крайних случая.

а) Пусть Земля — однородный шар. На расстоянии r от центра Земли снаряд испытывает притяжение только от внутренней части планеты радиусом r и массой M ( r ) = M ⊕( r/R ⊕) 3. Следовательно, он движется с ускорением

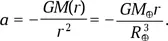
(знак минус говорит здесь о том, что направления векторов r и a противоположны). Как видим, это уравнение простых гармонических колебаний, возникающих в том случае, когда возвращающая сила пропорциональна отклонению тела от точки равновесия. В нашем случае эта точка — центр Земли.

Решить это уравнение можно по аналогии с уравнением малых колебаний маятника:

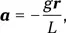
где g — ускорение свободного падения, L — длина маятника, r — его отклонение. Как известно, период колебания маятника составляет

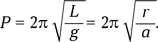
Значит, период колебания снаряда в шахте (независимо от амплитуды колебания!) составит

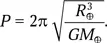
А полет между полюсами будет длиться

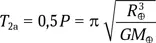
Таким образом, в случае однородной Земли снаряды прибудут к Южному полюсу одновременно ( Т 1= Т 2a).

Однако известно, что к центру Земли плотность увеличивается, поэтому рассмотрим другой крайний случай.

б) Пусть вся масса Земли сосредоточена в ее центре. Тогда ускорение снаряда

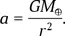
Это уравнение движения в поле точечной массы, типичное для тел Солнечной системы. Движение нашего снаряда по радиальной орбите можно представить как движение по вырожденному эллипсу с эксцентриситетом, практически равным единице. Тогда большая полуось этого эллипса равна R ⊕/2, а орбитальный период