Владимир Сурдин - Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике

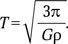
Это очень важная формула. Она показывает, что время оборота по низкой орбите зависит не от размера притягивающего тела, а только от его средней плотности.

Для поиска численных значений удобно помнить, что у низколетящего спутника Земли Т = 1,5 часа, а плотность Земли ρ ⊕= 5,5 г/см 3. Тогда для планеты плотности ρ получим: Т = 1,5 час 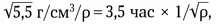если плотность измеряется в граммах на 1 см 3.

Зная плотность астероида, определим 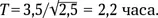Значит, вездеход не сможет объехать астероид за 2 часа. За такое время его нельзя облететь даже на ракете с выключенными двигателями. А с включенными? См. задачу 3.25 «Спасти космонавтов».

До сих пор мы предполагали астероид не вращающимся. Но если он вращается вокруг оси (а большинство астероидов вращается, и довольно быстро, с периодами в несколько часов), то, двигаясь в сторону, противоположную вращению, космонавты могли бы объехать астероид за указанное время, не оторвавшись от его поверхности.

Период колебания маятника в вакууме 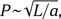где L — его длина, а — ускорение силы тяжести. Но при прочих равных условиях маятник в сопротивляющейся среде будет колебаться с бо́льшим периодом. Поэтому самыми быстрыми будут часы на Земле, а самыми медленными — лунные часы, помещенные в воздушную среду.

Если ракета будет лететь на низкой орбите по инерции, с выключенным двигателем, то двух часов ей не хватит, чтобы облететь астероид (см. задачу 3.23 «Объехать астероид»). Однако есть выход: гравитационной силе притяжения астероида можно «помочь», включив двигатель ракеты. При этом корабль должен быть направлен носом к центру астероида, а двигателем — от него. Давление двигателя увеличит центростремительное ускорение и сократит орбитальный период. Действительно, полное центростремительное ускорение a = V 2/ R , откуда 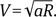Тогда орбитальный период на низкой круговой орбите 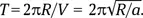Чем больше ускорение, тем короче период. Лишь бы хватило топлива.

Из условия задачи не ясно, начальному или текущему весу ракеты равна тяга ее двигателей. Поэтому рассмотрим оба варианта. Сразу после начала работы двигателей масса ракеты, а вместе с ней и ее вес начинают уменьшаться за счет выброса сгоревшего топлива. Поэтому тяга двигателей начнет сначала немного, а затем все больше и больше превышать вес ракеты, и она полетит.

Во втором случае предполагается, что тяга и вес постоянно равны. Но и в этом случае полет возможен, если ракета будет разгоняться горизонтально, пока не приобретет первую космическую скорость. Но если старт происходит на планете с атмосферой, то ракета должна быть очень прочной и термостойкой, чтобы не разрушиться от напора воздуха и не сгореть, как метеор.

Поскольку Солнце обращается вокруг центра Галактики со скоростью около 220 км/с, результирующая скорость корабля будет почти такой же и направленной в ту же сторону, что и у Солнца. Иными словами, орбита космического корабля не будет существенно отличаться от галактической орбиты Солнечной системы, и корабль никогда не попадет в центр Галактики.

Как показано в задаче 3.21 «Объехать астероид», время оборота на низкой орбите

Отсюда ρ = (3,5 час/ Т ) 2г/см 3. Например, из того факта, что ИСЗ на низкой орбите оборачиваются за 1,5 часа, следует, что средняя плотность Земли

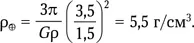
Казалось бы, все просто. Нужно лишь определить орбитальный период. Но как космонавты смогут это сделать? Ведь планета под ними вращается, поэтому ее ориентиры не годятся. Закройте книгу и подумайте.

Действительно, черная дыра, имея ничтожное сечение и практически не встречая сопротивления, будет падать к центру Земли почти свободно. А пройдя через него, она еще долго будет совершать затухающие колебания между диаметрально противоположными точками земной поверхности, пока не остановится вблизи центра планеты. За какое же время черная дыра впервые достигнет центра планеты?

Вспомним задачу 3.12 «К антиподам». Период обращения спутника на низкой околоземной орбите составляет

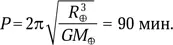
Свободный полет к центру Земли длится от 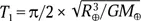до 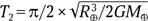в зависимости от степени концентрации ее вещества к центру. Следовательно, Т 1= 0,25 Р = 22,5 мин, а Т 2= 0,177 Р = 15,9 мин. Очевидно, для Земли это время составит около 20 минут. Именно столько будет падать черная дыра к ее центру, а отнюдь не мгновенно.

Если со стороны Луны мы видим практически полностью освещенный Солнцем диск Земли, значит, со стороны Земли в этот момент видна темная сторона Луны, иными словами — Луна близка к фазе новолуния. В декабре 1972 г. новолуние было в ночь с 5 на 6 декабря, а полнолуние наступило 20 декабря. Следовательно, это фото Земли было сделано при отлете от Земли к Луне. Дополнительно об этом свидетельствует внешний вид Земли: хорошо видна Антарктида с областью Южного полюса, т. е. наблюдатель был смещен к югу от экватора. Но так и должно быть, поскольку в декабре Солнце на эклиптике находится глубоко к югу от экватора, а Луна в новолуние расположена на небе рядом с Солнцем. Действительно, склонение Луны 6 декабря 1972 г. было −25,5°.