Вадим Романов - Прикладные аспекты аварийных выбросов в атмосферу

Значение F может быть связано с площадью нормального поперечного сечения струи и углом ее наклона к горизонту соотношения:

уравнение (3.79) при подстановке в него соотношения (3.80) приобретает следующий вид:

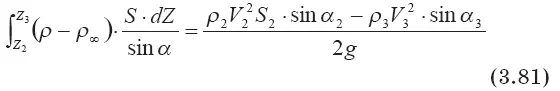
Достаточное условие преодоления струей инверсионного слоя толщиной ΔZ запишется так:

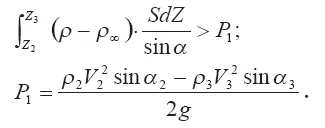
Динамическая высота подъема струи Z dвнутри задерживающего слоя ΔZ=Z 4-Z 2определится из соотношения (W 3=0):

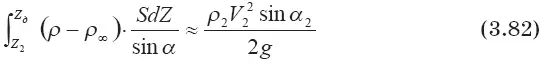
Процедура определения высоты подъема струйного выброса в общем случае его движения в стратифицированной атмосфере точно такая же, как и для кратковременного выброса. Только вместо уравнения (3.78) надо использовать уравнение (3.82).

Проведенный выше анализ показывает, что подъем выбросов в реальной атмосфере будет обязательно прерван на некоторой высоте.

Потеря выбросом динамической индивидуальности на фоне турбулентных движений атмосферы не означает, что его вещество полностью идентично веществу окружающей среды. После достижения выбросом максимальной высоты подъема Z gвыброс начинает «растаскиваться» турбулентными вихрями атмосферного воздуха. Его форма уже не может быть моделирована простым геометрическим телом типа сферы или эллипсоида. Вещество выброса подвержено воздействию турбулентных движений атмосферы и стабилизирующему воздействию температурного градиента, возвращающему его к компактной конфигурации.

Естественно, что в этих условиях возникший объем не может рассматриваться как единое динамическое целое — он занимает слишком большие пространственные размеры и имеет поверхность сложной флуктуирующей формы. Для анализа дальнейшего всплытия его вещества, температура которого отлична от Т ∞, естественно рассматривать динамику отдельных молей или квазиклубов его вещества, на которые он распался.

Аналогичным образом происходят процессы теплопереноса на участке затухания динамической активности струй. Если атмосферные условия устойчивые, то струйный поток, потерявший свою динамическую индивидуальность при завершении подъема, имеет температурную (и концентрационную) неоднородность и способен продолжать восходящее движение.

Отметим, что подобные температурные (концентрационные) неоднородности продолжают свое поступательное движение в ветровом потоке, являясь фактически динамически пассивными. Рассмотрим оба этих случая.

Стабилизаиия вещества разрушившегося клуба

Назовем фрагменты разрушившегося выброса термоклубами или термооблаками (сокращенно — облаками). В дальнейшем будут использованы оба этих названия.

На завершающем участке подъема подобного выброса изменением кинетической энергии можно пренебречь по сравнению с изменением его внутренней энергии. При этом справедливо уравнение баланса этой характеристики, как для выброса в целом, так и для отдельных его термоклубов.

Внутренняя энергия термоклуба при его подъеме с высоты Z 1до высоты Z 2может измениться только за счет охлаждения вовлеченным воздухом. Для моментов времени t tи t 2(соответствующих высотам Z tи Z 2) можно записать следующее соотношение:

(MΨ) 2=(MΨ) 1+M e·Ψ ∞(3.83)

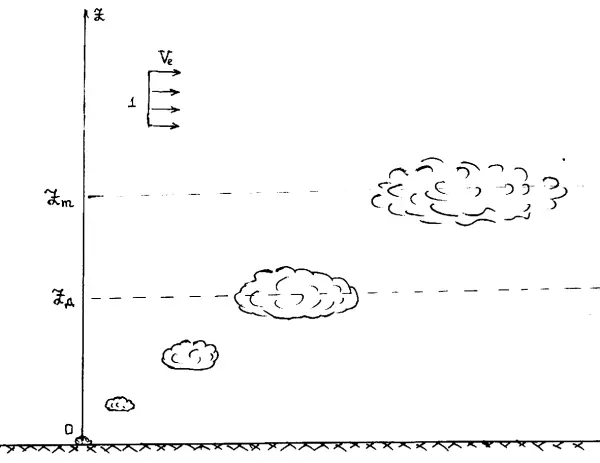
Рис. 3.19. Схема эволюции кратковременного выброса в ветровом потоке: 0 — место инцидента; 1 — ветер; Z g— высота потери выбросом динамической индивидуальности; Z m— высота стабилизации вещества выброса.

В этом соотношении:

Ψ = h + gZ; 'Ψ ∞=h ∞+gZ;

где h = С р— Т — статическая энтальпия единицы массы облака; М,М е— масса облака и масса вовлеченного в него воздуха; h ∞= С рТ ∞— статическая энтальпия ед. массы окружающего воздуха.

Разделим обе части (3.83) на ΔZ при учете вида h и считая С р≈ С р∞:

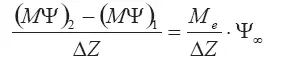
В дифференциальной форме это уравнение записывается так:

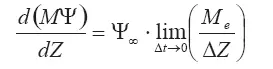
Используя соотношение для вовлечения 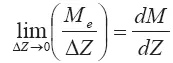, приходим к следующему уравнению:

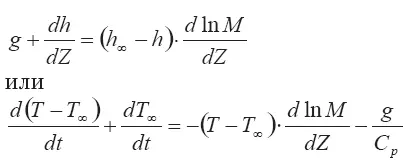
Обозначим дефект температуры клуба

Т — Т ∞= θ

и перейдем к высотной координате, используя соотношения

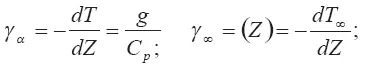
Получаем:

Постоянная С находится из условия: при Z=Z gu=u gпри задании конкретных значений γ ∞(Z) и M(Z), являющихся сложными функциями высоты Z.

Вводя как в работе [132] удельную скорость вовлечения

представляющую собой массу вовлекаемого воздуха, отнесенную к единице высоты Z, получаем для М следующие выражение:

М = е αZ

Рассмотрим вначале случай постоянных значений α и γ ∞.

Подставив это выражение для массы облака в формулу (3.84) при γ ∞= const и α = const, получаем:

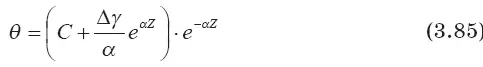
Находим постоянную интегрирования:

при Z=Z g θ = θ g

откуда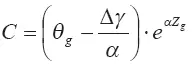

И окончательное выражение для дефекта температуры термоклуба получаем при подстановке постоянной С в уравнение (3.85):

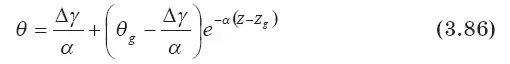
Эта формула при Z g= 0 совпадает с формулой работы [132], полученной в предложении сохранения потенциальной температуры воздушной частицы при ее адиабатическом смещение вдоль оси Z и при задании исходного уровня Z=0 и начального перегрева θ 0=Т 0— Т ∞.