Вадим Романов - Прикладные аспекты аварийных выбросов в атмосферу

Высота стабилизации вещества облака из соотношения (3.86), определяемая из условия 0=0, находится при подстановке вместо Z его предельного значения Z m.

Поучаем

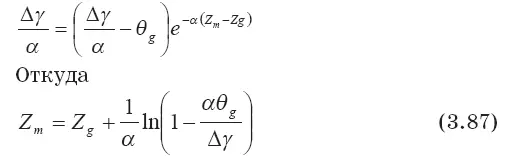
Это выражение является обобщением формулы Л. Махты для высоты стабилизации выброса в атмосфере, которое учитывает процесс неадиабатического расплывания выброса, начинающийся с уровня Z g— высоты потери его динамической индивидуальности.

Формула Л. Махты [127]:

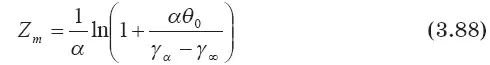
где θ 0— разность потенциальных температур на исходном уровне Z = О, дает аналогичные значения для Z m.

Формула (3.87) имеет смысл при Δу < О, т. е. при устойчивом состоянии атмосферы, когда температура воздуха уменьшается с высотой медленнее, чем на 1 градус на каждые 100 метров.

При этом

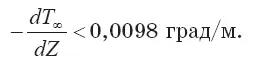
На графиках Рис. 3.20 представлено сравнение результатов расчетов высот подъема взрывных выбросов Z mв зависимости от начального перегрева вещества клуба, выполненное по различным формулам. Отметим, что формула (3.87) при Z = 0 и θ g0=Т 0-Т ∞дает значения высот подъема взрывных клубов такие же, как по формуле Л. Махты.

Расчеты выполнялись для следующих условий[132]: α =5 × 0 -41/м (вовлечение 1 кг воздуха на каждые 4 кг облачного воздуха при подъеме его на 500 м) при вариации коэффициента γ ∞.

Как следует из графиков этого рисунка, формула Сэттона дает заниженные значения для Z mпри любых начальных перегревах вещества выброса. Этот факт отмечается и в работе [132], где кроме этого подчеркивается качественное согласие результатов расчетов по формуле Махты с экспериментальными данными по высотам стабилизации облаков ядерных взрывов. Расчеты по формуле (3.87) показывают очень сильную зависимость Z mот степени устойчивости атмосферного воздуха, что является физически правдоподобным.

Для получения выражения для высоты стабилизации выбросов в реальной атмосфере [152] следует исходить из наличия турбулентных пульсаций температуры атмосферного воздуха 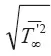и переменных по высоте выброса значений коэффициентов вовлечения и γ ∞.

Будем исходить из уравнения (3.83а) при учете связи вовлечения Е в произвольный объем с его боковой поверхностью S δи изменением массы облака по времени

где удельное вовлечение Е для нагретого вещества выброса, поднимающегося со скоростью W в атмосфере записывается так:

S δ— площадь поверхности термоклуба через которую происходит вовлечение окружающего воздуха; ς — коэффициент вовлечения.

Не ограничивая общности рассуждений, можно считается термоклуб сферическим.

Тогда

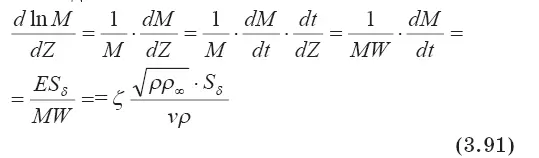
где ν — объем термоклуба

При получении этого выражения была использована связь:

Подставляя вместо S δи их значения в формулу (3.91), получаем:

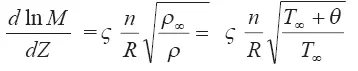
При получении этого выражения было использовано условие изоабатичности течения. Коэффициент n учитывает соотношение боковой поверхности и его объема. Если R — радиус эквивалентной сферы, имеющей объем нагретого облака, то n = 3.

Уравнение для определения дефекта температуры термоклуба на высотном уровне стабилизации его вещества запишется в окончательной форме:

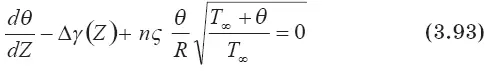
Это уравнение может быть решено численно. Для получения приближенного его решения воспользуемся условием малости θ:

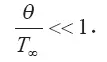
Тогда уравнение (3.93) приобретает приближенный вид:

Его решение записывается так:

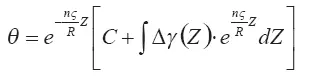
Постоянная С определяется из начального условия для дефекта температуры на уровне потери клубом динамической индивидуальности: при Z = Z gθ = θ g

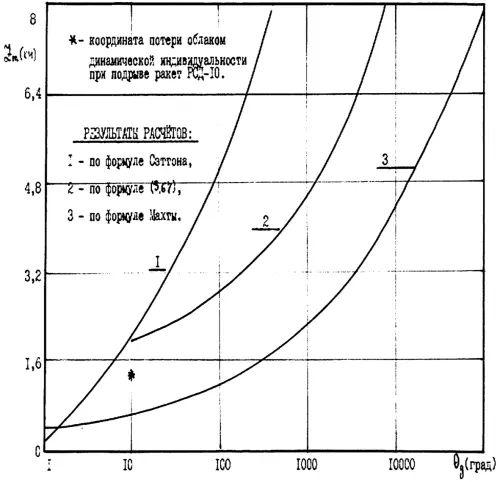
Рис. 3.20. Высота подъема облака взрыва в зависимости от начального перегрева θ g=T 0— Т ∞.

Откуда получаем

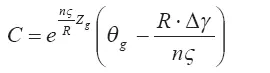
Окончательно для перегрева вещества распавшегося выброса получаем выражение:

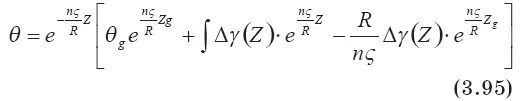
Подставляя вместо γ ∞(Z) конкретные значения профиля градиента атмосферной температуры как функции высоты Z, можно получить связь перегрева вещества выброса с его геометрической высотой и с высотой потери им динамической индивидуальности. В частности высота стабилизации вещества клуба в турбулентной атмосфере найдется из соотношения (3.95) при задании на этом высотном уровне значения дефекта температуры вещества клуба в виде: при Z = Z mθ = θ m, где .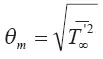

Особенно простой вид имеет выражение для перегрева вещества распавшегося клуба как функции высоты при постоянном значении градиента атмосферного воздуха. Из (3.72) получаем:

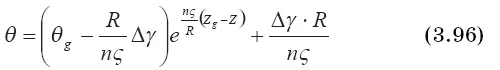
Формула (3.96) совпадает с формулой (3.85) при связи коэффициентов вовлечения ς, удельной скорости вовлечения α и коэффициента формы n в виде следующего соотношения

Отметим, что соотношение (3.96) может быть получено при использовании формулы (3.86) и определений α и Е.