Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Грядущий климат во многом будет зависеть от человеческой деятельности. Хотя потепление в ХХ веке составило лишь полградуса, в XXI веке расчеты предсказывают изменение уже на несколько градусов (от 1 до 4 °C в соответствии с предполагаемыми сценариями). Расчеты недостаточно надежны, чтобы точно определить последствия деятельности человека для климата, но крайне маловероятно, что они окажутся несущественными. В частности, потепление приводит к значительному повышению уровня Мирового океана (который уже растет на 3 мм ежегодно, по данным с 1990 по 2010 год). Это происходит из-за таяния ледников и других более сложных и, вероятно, более серьезных последствий.

Согласно сообщениям МГЭИК, с 1970 года экстремальные явления, такие как жара и сильные осадки, значительно участились. Аналогичная тенденция наблюдается во многих регионах в отношении засухи, а в некоторых – и в отношении тропических циклонов. Еще один весомый аргумент, который касается засухи и осадков, заключается в следующем: если повысится средняя температура, следует ожидать, что увеличатся и перепады температуры и, следовательно, конвективные движения станут более интенсивными. Это коснется, например, ячеек Хэдли (см. илл. 9) и сопутствующих им пассатов. Таким образом, последствия таких конвективных движений проявятся намного сильнее: влажные зоны станут еще более влажными, а засушливые районы – более сухими.

Удастся ли человечеству остановить это повышение температуры? Сокращение выбросов парниковых газов сопряжено с экономическими и социологическими трудностями, которые не рассматриваются в нашей книге. В то же время следует отметить осознание этой проблемы, что воплотилось в создании упомянутой выше МГЭИК. Эта объединяющая ученых со всего мира и консультирующая правительства организация уникальна. В 2007 году МГЭИК получила Нобелевскую премию мира.

Что может быть банальнее горки песка? А ведь этот гранулированный материал обладает неожиданными свойствами! Убедиться в этом можно и без лабораторного оборудования: например, поставить опыты с помощью обычной кухонной утвари. Ну а счастливчики могут отправиться на пляж!

Британский физик Осборн Рейнольдс (1842–1912) был выдающимся специалистом по гидродинамике. Возможно, благодаря изучению движения приливов во время его прогулок по пляжу? Однажды он сделал следующее наблюдение, которое впоследствии представил на конгрессе Британской ассоциации в 1885 году: «Когда нога надавливает на песок, плотный после ушедшего прилива, участок, находящийся вокруг ноги, тотчас же становится сухим… Надавливание ноги разрыхляет песок, и чем сильнее оно, тем больше воды уходит… Оно делает песок сухим до тех пор, пока снизу не прибудет достаточное количество воды» (илл. 1). По словам Рейнольдса, давление, оказываемое ногой, вызывает разрыхления песка, и в результате вода уходит в зазоры между окружающими песчинками, поэтому песок и становится сухим.

Это явление разрыхления кажется противоречащим здравому смыслу. Почему давление увеличивает пространство между песчинками, тем самым заставляя воду уходить? Ответ связан со структурой этой смеси воды и песка. Для простоты мы предположим, что песчинки сферические и одинаковые, и это приведет нас к задаче об укладке твердых шаров. А далее в этой главе мы зададимся вопросом, как укладывать атомы…

Можем ли мы заполнить все пространство твердыми шарами? Очевидно, нет, поскольку между ними всегда будет оставаться некоторое свободное пространство. Объем пространства, занимаемого шарами, определяет плотность упаковки. Чем меньше свободного пространства между ними, тем компактнее и плотнее эта упаковка. Как получить максимальную плотность при упаковке идентичных твердых шаров? Ответ на этот вопрос прояснит тайну песка, высыхающего под стопой.

1. Вокруг стопы, давящей на песок, возникает сухая область

Для начала рассмотрим аналогичную задачу, но на двумерном, а не трехмерном пространстве: как разместить одинаковые диски в плоскости. Для начала возьмем три диска. Наиболее компактной упаковкой будет являться такая, когда каждый диск касается двух других, то есть центры всех трех дисков образуют равносторонний треугольник. При наличии большего количества дисков наиболее компактная упаковка получается путем объединения таких групп, составленных из трех дисков (илл. 2a). Предлагаем читателю рассчитать долю площади плоскости, покрытой дисками: она равна 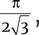или 90,7 %. Интересно сравнить этот случай с покрытием, изображенным на илл. 2b, где доля площади, занимаемой дисками, составляет лишь π/4, или 78,5 %.

Интуиция подсказывает, что именно такая упаковка, как на илл. 2а, наиболее компактная из всех возможных. Каждый диск касается еще шести, и невозможно сделать так, чтобы он касался большего количества дисков. Тем не менее тот факт, что количество точек соприкосновения между дисками является максимальным, еще не является достаточным доказательством того, что пространство, занимаемое заданным числом дисков, минимально. Точное доказательство было найдено лишь в XX веке.

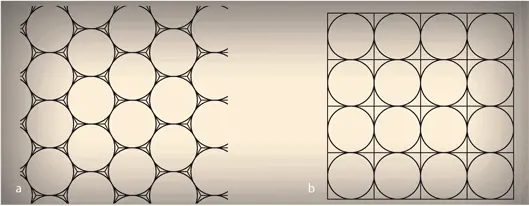
2. Два типа упаковки одинаковых дисков на плоскости. a.Наиболее компактная упаковка. b.Менее компактная упаковка, при которой диски вписываются в квадратную сетку

Можно заметить, что диски при наиболее компактной упаковке могут быть вписаны в шестиугольники, которые полностью покрывают плоскость, – как, например, терракотовая плитка (илл. 2а): в таком случае говорят, что происходит «замощение» плоскости шестиугольниками. Именно такое мощение шестиугольниками осуществляют пчелы для постройки сот (илл. 3). Есть лишь два других способа замостить плоскость одинаковыми правильными многоугольниками: квадратами (илл. 2b) или треугольниками (илл. 4).

3. Создавая соты, пчелы выстраивают их шестиугольниками. Возможно, такое расположение максимально удобно для личинок. К тому же оно экономит воск. В самом деле, длина границ, разделяющих области равных площадей, будет наиболее короткой при упаковке правильными шестиугольниками