Анатолий Ахутин - История принципов физического эксперимента от античности до XVII века

Определяемость предмета числом, тождество принципа понимания с принципом красоты при космическом (онтологическом) понимании самой прекрасной (идеальной) формы — все это превращало художественную практику античности в «экспериментальную базу» или основание для теоретических спекуляций 39 . Сошлемся на однажды уже процитированное высказывание Платона (стр. 29). Вообще нет недостатка в многочисленных свидетельствах этой роли художественной практики. Широко известен «канон» Поликлета, который дал в своей статуе «Дорифор» как бы универсальный образец абсолютных пропорций человеческого тела. Эта идея определяющей роли пропорции оставалась ведущей на протяжении длительного времени. Филон Александрийский в своей «Механике» приводит слова Поликлета: «Успех (художественного произведения) получается от многих числовых соотношений, причем любая мелочь может его нарушить». «Очевидно,— добавляет Филон,— таким образом и в данном искусстве (механике) при создании сооружений с помощью множества чисел приходится делать в результате большие ошибки, если допустить хотя бы малую погрешность в частных случаях» 40 .

Форма, строго определенная пропорциональными отношениями, вещественная, техническая, механическая, конструктивная форма, форма очень четкая, заметная в каждой ноте, не терпящая даже малейшего отклонения от закона,— таково определение античной красоты, и мы видим, что оно совпадает с определением научно зафиксированного объекта

Таким образом, теоретически-наблюдающее мышление вырабатывало свои приемы и методы, формировало свою технику в эстетической сфере — в музыке, в метрике мелического искусства, в архитектуре и скульптуре. Принципы структуры, оформленность, созвучия, равновесия, симметрии — вот то, что формирует технические средства рождающегося научного познания. Обоснованное в самом себе и завершенно оформленное — вот подлинное бытие, которое для античности составляет интеллектуально постижимую сущность бытия и которое одно только понятно античному мыслителю. Античный эквивалент экспериментирования ближе всего стоит к выбирающей, прикидывающей, сообразующей и оформляющей деятельности художника. Можно привести здесь еще одну прекрасную характеристику пифагорейского метода, данную А. Ф. Лосевым: «Пифагорейский глаз все время как бы обмерял разные вещи, стремясь найти между ними наглядно и структурно видимую аналогию» 42 .

Теперь, после того как мы получили некоторое представление о всем своеобразии пифагорейской трактовки числа, вернемся к его конкретной форме.

Мы начали с проблемы некоего логического круга, заключающегося в том, что тело определяется как число, число же опять-таки есть тело. Теперь понятно, что под числом разумеется та форма тела, в которой оно представляется мыслящему взору как тело самой формы,— не столько оформленное тело, сколько воплощенная форма; тело мыслимое (видимое) в идеальности его формы, и форма, сущая с реальностью тела. Наблюдение, сосредоточиваясь на различении того, что «есть само по себе», восходит к принципу формы, числу и, далее, к принципу самого числа — единице. Наблюдение становится мыслящим. Мышление же остается созерцанием 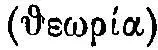, а единица — формой. Круг этот никогда не сжимается в точку, а лишь по-разному проходится. В нем и заключена своеобразная экспериментальность, присущая античному теоретическому мышлению.

Только теперь мы сможем понять, почему единица не считается числом и каков смысл следующего ее определения в VII книге Евклидовых начал: «Единица есть то, через что каждое из существующих считается единым» 43 . Не наша задача вскрывать противоречивость этого определения. Но после сделанных разъяснений становится ясным, что здесь под единицей разумеется как раз та идеальная форма, которая делает вещь самой собой и определяет ее как тождественную себе форму. Ясно также, почему число легко отождествляется с сущностью вещи. Ведь даже для того, чтобы только считать одинаковые предметы, например, дома, надо уже уметь выделять дом как таковой среди других предметов, надо уметь распознавать чистую, существенную форму дома, т. е. принцип отождествления разных домов как домов. Это — существенная форма вещи, которая как идеальная форма может не быть тождественной ни одному экземпляру данного вида и вместе с тем составлять принцип их отождествления. Разумеется, два дома есть число, но один дом не является числом. Единицы, таким образом, для пифагорейцев разновидны и разнокачественны. Феон Смирнский говорит: «Если в области зримых предметов происходит деление единицы, то она как тело уменьшается и разделяется на меньшие части, но в числовом отношении она увеличивается, так как место одной вещи занимает теперь несколько вещей» 4

Каждое отдельное число может быть рассмотрено как своеобразная единица, т. е. как определитель некоторой идеальной формы. В этом смысл самого архаического представления чисел треугольными, квадратными, пятиугольными, прямоугольными формами.

Такое изображение чисел любопытно во многих отношениях. Прежде всего, классификация чисел по геометрическим фигурам есть как бы классификация основных структурных элементов для построения любого правильно образованного объекта, так сказать инструментарий. Какие же особенности сразу бросаются в глаза? Классификация ведется по осям симметрии. Любое треугольное число соответствует оси третьего порядка, квадратное—четвертого и т. д. Это характеризует первоначальную операцию отождествления подобных вещей и прежде всего отождествление вещи с самой собой при ее преобразовании в себя. Вращение, круговое движение сначала выделяет центр тела. А эта операция, нахождение середины, центра, как мы неоднократно будем убеждаться, является для античности важнейшей, будет ли это центр симметрии, центр тяжести, центр равновесия или какой угодно иной центр 45 .

Во вращении вместе с тем тело определяется в его симметрической структуре и потому может определяться треугольным, квадратным или иным соответствующим числом. Итак, отождествление тела с самим собой в преобразовании вращения зафиксировано в фигуре числа.

Но, как говорил Филолай в цитированном месте (стр. 32), число определяет тело также по природе гномона, т. е. по природе части, прибавление которой осуществляет преобразование подобия. Таким образом, пифагорейцам была известна и операция отождествления тела по чистой фигуре при изменяющейся величине.

Что точечно-геометрическое изображение чисел есть в равной мере запись определенной операции, ясно из того, что при таком изображении автоматически выполняется построение некоторого пропорционального ряда 46 . Вместе с тем, анализируя это последнее преобразование подобия, мы подошли к самому важному принципу пифагорейского конструирования — к принципу пропорции 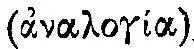Поскольку преобразование с помощью гномона — дискретное преобразование, предметы уподобляются не непосредственно, а в некотором пропорциональном отношении. И оно является также способом их упорядочения и структурирования.