Анатолий Ахутин - История принципов физического эксперимента от античности до XVII века

Именно с этим вопросом столкнулось исследование музыкальной гармонии. Октава (отношение высот 2:1) представляет собой как бы модель гармонии, в которой дана первоначально лишь относительная мера (интервал) высоты звука 64 . Проблема деления октавы потому и стала центральной проблемой пифагорейского учения о гармонии, что в ней сосредоточена та самая теоретически-конфликтная ситуация, о которой образно говорит Платон. И все разнообразие греческих музыкальных теорий развертывается вокруг проблемы деления, тона, поскольку оказывается невозможным найти абсолютную меру, чистую единицу (атом) звука. Теоретическое «ухо» различает иррациональный шум в самой сущности звука, в средоточии гармонии. Это — экспериментальный факт: он обнаружен теоретическим «слухом» и даже является отрицательным по отношению к исходной идее. И он привел к изменению теории. Первоначальное дискретно-арифметическое понимание числа вытесняется геометрическим, и постепенно геометрическая алгебра сосредоточивает в себе все конструктивные проблемы. Арифметика же сводится к искусству вычислять.

Если не считать таких фундаментально-космологических противоположностей, как предел и беспредельное, или философско-всеобщих формулировок типа: единое — многое, оформленное — аморфное, если присмотреться к конкретной форме этого «неподобия», как она представлена в математических объектах, то мы обнаружим следующие факты.

Однородные числа можно сопоставлять различным отрезкам, так это делается, например, у Евклида 65 . Существенная неоднородность свойственна плоским фигурам, не связанным преобразованием подобия (т. е. не отвечающим однородным числам: треугольным, квадратным и т. д.). Для них оказывается необходимым найти посредствующую фигуру, одна из сторон которой составляла бы со сторонами уподобляемых фигур непрерывную пропорцию. Если дело касается телесных (трехмерных) фигур, то для уподобления совершенно неподобных тел необходимы уже два посредствующих члена, т. е. непрерывная пропорция, представляющая уравнение третьей степени. Первая задача является центральной для всей античной геометрии, а решение второй приводит к разработке стереометрических методов, учения о конических сечениях и статической механики. Платон в «Тимее» делает любопытное замечание: «...если бы телу вселенной надлежало быть только плоским, без всякой толщины, тогда достаточно было бы и одного среднего члена для того, чтобы он мог связать и два другие между собой 66 . Но так как ему надлежало быть массообразным, трехмерно-телесным, массы же никогда не соединяются посредством одного и всегда при посредстве двух средних членов, то бог, поместивши в средине между огнем и землею воду и воздух и приведя (все эти элементы), сколько возможно, в такое пропорциональное друг другу отношение, в котором как огонь относится к воздуху, так воздух к воде, и как воздух относится к воде, так и вода к земле, тем самым связал их воедино и таким образом устроил видимое и осязаемое небо» в7 7 Поскольку античной науке ко времени Платона было известно пять правильных многогранников, Платон принял куб в качестве начала земли (и начала осязания), тетраэдр в качестве начала огня (и начала зрения) и в таком случае водяной икосаэдр и воздушный октаэдр оказывались посредствующими фигурами, связывающими куб и тетраэдр. Додекаэдр соответствовал космосу в целом. Далее уже нетрудно было сопоставить этой пропорции интервалы октавы. Такова конкретная картина всепронизывающей гармонии античного космоса, как она конструируется в «Тимее». Мы вкратце изложили здесь это учение 68 , чтобы показать по существу простой и единый механизм формирования предмета в греческом теоретическом мышлении.

Построения, считающиеся обычно прихотливыми фантазиями мистических спекуляций Платона, оказываются глубоко технологическими и по-своему строжайшим образом связанными с экспериментированием (теоретическим наблюдением) эпохи классической греческой античности.

*

Конфликт между теоретически-понятийной стороной (тело есть число) и предметной стороной (число есть тело) не просто констатируется, а теоретически формулируется пифагорейцами в проблеме несоизмеримости. Это — радикальная апория, связанная с попыткой понять тело числом. Предпосылка (истоки ее мы не исследуем) , согласно которой мир постигается числом, позволяет подойти к миру теоретически и познавать его (исследовательская сторона). Но вместе с тем в процессе развертывания такого понимания и благодаря нему открываются его внутренние границы. Это и составляет экспериментальное содержание проблемы несоизмеримости: радикальное неподобие, разнокачественность, разноначальность космоса, т. е. невозможность охватить его единой гармонией (привести в отношение подобия все неподобное), невозможность установления универсальной единицы — иными словами, невозможность понять его средствами пифагорейского арифметизма.

Эксперимент и математическая теория

К концу V в. до н. э. математические исследования греческих ученых достигают чрезвычайно высокого уровня. С точки зрения нашей темы нас интересуют в этом процессе три момента:

выработка новых приемов и способов мысленного конструирования объекта;

выдвижение математики в качестве образца чисто теоретического знания и критика в связи с этим нематематического знания (Платон);

внедрение в геометрию механических способов решения задач, первый контакт между геометрией и механикой.

По мере развития арифметики, геометрии, астрономии и гармонии — четырех основных теоретических дисциплин эпохи классической античности — неизбежно возникает проблема единства теоретического знания и его автономии, проблема, составляющая одну из основных тем платоновской эпистемологии. Однако с полной определенностью эта проблема была поставлена элеатами уже в самом начале V в. до н. э.

Пифагорейский принцип, согласно которому число или форма составляют единое начало бытия и познания предмета и космоса как гармонического единства этих единиц, уже нес в себе проблему формы форм (единицы единиц), т. е. необходимость отыскать форму, заключающую в себе свойства всевозможных форм.

Проблема единого (универсальной единицы) выдвигается на первый план, причем единое сразу же осознается так же и как всеобщая форма, и как бытие само по себе 69 . Однако нас интересует не онтологическая, а конструктивная сторона проблемы.

Мы уже говорили, что переход от первоначального арифметизма пифагорейцев к геометрической алгебре связан с проблемой несоизмеримости. Несоизмеримость, осознанная как принципиальная трудность в отыскании универсальной единицы, была по существу для пифагорейцев экспериментальным затруднением. Благодаря несоизмеримости, многообразие чисел-предметов распадалось в конечном счете на множество качественных единиц, не могущих находиться друг к другу ни в каком разумном отношении 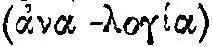. Иными словами, об этих фундаментальных качественных единицах уже не могло быть никакого теоретического знания. Они невыразимы 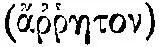по отношению друг к другу 70 . Парадокс, обострившийся еще в результате критики со стороны элеатов, состоял в том, что универсальная единица как начало всех чисел должна в потенции содержать все несоизмеримые величины В этой ситуации чрезвычайно важным шагом была разработка методов геометрической алгебры как способа взаимно соотносить и, следовательно, соизмерять (уподоблять) непосредственно несоизмеримые (неподобные) числа. Эта проблема породила метод приложения площадей и затем — венец греческой математики — теорию конических сечений, ставших основными проблемами античной геометрии п .