Анатолий Ахутин - История принципов физического эксперимента от античности до XVII века

Рассмотрение «выразимости» непосредственно несоизмеримых единиц, классификация и систематизация на этой основе чисел, включая и иррациональные, составляет заслугу математиков начала IV в. до н. э. Феодора и Теэтета, о которых рассказывает Платон в своем диалоге «Теэтет» 73 . Простейшим способом «выражения» иррациональной единицы, например Т^З, является рассмотрение ее как стороны квадрата с площадью три квадратные i единицы. Соответственно и две «единицы», несоизмеримые друг с другом, могут быть сопоставлены по производимым ими площадям. В X книге евклидовых «Начал» 74 такие отрезки называются «выразимыми». Кроме того, здесь исследуются и более сложные формы «выразимости», которые были затем использованы при построении теории правильных многогранников (XIII книга «На| чал»). «Все эти доказательства,— пишет Ван дер Варден,— базируются на одной и той же мысли, которая красной нитью проходит через всю книгу: чтобы показать свойства каких-либо отрезков, строят на этих отрезках квадрат и исследуют свойства этого квадрата» 75 .

Представив иррациональное число как диагональ квадрата или как сторону квадрата, площадь которого не является квадратным числом, греческий математик имел совершенно точное изображение иррационального. Это обстоятельство только укрепляло в , мышлении греков их геометро-наглядный метод, так что Платон по праву мог назвать геометрию, мышление в формах, наукой о том, «как сделать соизмеримыми на плоскости числа, по своей природе несоизмеримые» 76 .

Развитие идеи выразимости в видимых (геометрических и стереометрических) фигурах некоторых скрытых и самих по себе несравнимых элементов чрезвычайно важно и характерно для теоретического мышления эпохи античности вообще. В этом математическом методе наглядно представлены, механизм и как бы схема способа, которым античные мыслители превращали предметное наблюдение в теоретический анализ. Будет ли это атомистическая теория Демокрита или проблема отношения между структурой тел и структурой идей у Платона, или же, наконец, теория 1 Аристотеля о выразимости структуры предметных потенций 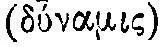в актуальной структуре предмета 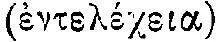— везде мы имеем дело с одним и тем же ходом мысли, который является действительным развитием первоначального метода пифагорейцев. Анализ предметных структур как статических симметрий (числа), дополняемый внетеоретическим динамизмом (натурфилософия числа), осмысляется теперь таким образом, что в понятии выразимости сам момент динамики получает теоретическое истолкование.

Мы не имеем здесь возможности продемонстрировать всю фундаментальность этой особенности греческого мышления в других сферах античной культуры. Сошлемся лишь на два исследования. В книге А. Сабо «Начало греческой математики» подробно показана глубокая связь математической терминологии с терминологией музыкальной практики. Исследователь античной архитектуры Д. Хэмбидж демонстрирует элементы динамической симметрии в античной пластике". Анализируя большой искусствоведческий материал, Хэмбидж показывает, как в структуре основных архитектурных элементов Парфенона и других греческих храмов реализуется принцип динамической симметрии. Статический и замкнутый в себе квадрат он противопоставляет прямоугольным элементам с диагональю 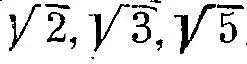и т. д., показывая, как их структура необходимо развертывается в более сложную систему, захватывая своими связями все сооружение.

Таким образом переход от статично-симметричного арифметизма ранних пифагорейцев к динамической геометрии эпохи Платона свидетельствует о значительном развитии конструктивных средств и, следовательно, экспериментально-теоретической способности вообще. Дело, однако, осложняется следующим обстоятельством. Геометрическая форма, взятая как способ выражения некоторой предметной, качественной единицы, оставшейся за рамками самой геометрии, отделяется от объекта. Чистая и автономная геометрия, ставшая впервые собственно математической дисциплиной, рассматривается сама по себе вне зависимости от возможного применения к физическим объектам.

Вместе с тем, коль скоро именно геометрический образ является теоретическим выражением объекта, чисто математическое исследование свойств пропорций или геометрических фигур представляется достаточным и необходимым способом теоретического представления предмета.

Такова предпосылка платоновского априоризма в теоретическом мышлении. Но именно благодаря этому Платон глубже понял значение и смысл отношения математики к предметному исследованию.

«...Когда они (математики.— А. А.) ...пользуются чертежами и делают отсюда выводы, их мысль обращена не на чертеж, а на те фигуры, подобием которых он служит. Выводы свои они делают только для четырехугольника самого по себе и его диагонали, а не для той диагонали, которую они начертили... То же самое относится к произведениям ваяния и живописи... они служат лишь образным выражением того, что можно видеть не иначе, как мысленным взором» 78 . Фундаментальная мысль о том, что наши теоретические утверждения относятся к идеально-сущностному образу вещи, а не к ее эмпирически воспринимаемому единичному и случайному образу, пронизывает многие рассуждения Платона. Собственно говоря, важнейшим моментом центрального учения Платона об «эйдосах», или об «идеях», и является понимание того, что геометрическая, идеальная форма вещей, видимая очами разума, и есть цель и результат теоретического определения вещи Она обладает теоретическими качествами всеобщности, необходимости и неизменности в противоположность случайности, неопределенности и произвольной изменчивости предмета непосредственного наблюдения.

Поскольку, таким образом, оказывается, что собственно математические исследования, исследования формы как таковой, с одной стороны, не зависят от неточности (неуловимости) чувственных впечатлений, а с другой дают непосредственно предметный результат, становится понятен тот теоретико-математический энтузиазм, который так характерен для Платона в отличие от Аристотеля 80 .

Со своей идеальной высоты Платон подвергает резкой критике непоследовательное смешение математики и эмпирии у ранних астрономов и музыкантов. «Эти узоры на небе, украшающие область видимого,— говорит он,— надо признать самыми прекрасными и совершенными из подобного рода вещей, но все же они сильно уступают вещам истинным... Это постигается разумом и рассудком, а не зрением... Небесным узором надо пользоваться как пособием для изучения подлинного бытия...» 81 Понятно, что при таком настроении Платон и на пифагорейцев смотрит как на эмпириков: «Клянусь богами, у них это выходит забавно: что-то они называют «уплотнением» и настораживают уши, словно ловят звуки голоса из соседнего дома; одни говорят, что различают какой-то отзвук посреди, между двумя звуками и что как раз тут находится наименьший промежуток, который надо взять за основу для измерений, другие спорят с ними, уверяя, что здесь нет разницы в звуках, но и те и другие ценят уши выше ума.— Ты говоришь о тех добрых людях, что не дают струнам покоя и подвергают их пытке, накручивая на колки...— Они,— заключает Платон, имея в виду пифагорейцев-эмпириков,— ищут числа в воспринимаемых на слух созвучиях, но не подымаются до рассмотрения общих вопросов и не выясняют, какие числа (курсив наш.— А. А.) созвучны, а какие — нет и почему» 82 .