Анатолий Ахутин - История принципов физического эксперимента от античности до XVII века

Таким образом, наши предки, обратив внимание на эти явления природы, взяли с них примеры и, подражая им, под божественным наитием создали целесообразное применение к жизни их принципов» 42 . Посмотрим далее, как Витрувий определяет машину: «Машина есть система связанных между собою частей из дерева, обладающая наибольшей мощностью для перемещения тяжестей. Сам же этот механизм приводится в действие посредством круговых вращений искусным приемом, называемым у греков 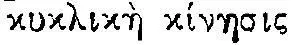43 . В третьей главе той же книги Витрувий анализирует множество механизмов и, находя в каждом рычаг и тягу в качестве основных элементов, приходит к выводу: «Вот так же, как и взятые нами для примера предметы получают свое движение в отношении какого-то центра путем совмещения принципов прямолинейного и вращательного движений, так вот теперь и повозки, коляски, тимпаны, колеса, винты, скорпионы, баллисты, прессы и прочие машины — все достигают предназначенного эффекта, действуя по тем же принципам, т. е. в отношении определенного центра силой прямолинейного движения и ротации» 4 \

Таким образом, схема: машина (потенция, 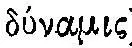) — рычаг — весы — «система кругов» 45 , на протяжении всего развития эллинистической механики служила методом отыскания причин и начал механического искусства. В результате рычаг выступал в качестве теоретической идеализации механического орудия-инструмента (органа) вообще, в качестве того орудия орудий, который непосредственно переводит естественное движение руки в систему насильственных движений механического искусства.

Автор «Механических проблем» анализирует на этом основании функционирование корабельного весла (гл. V), руля (гл. VI), мачты (гл. VII), колеса (гл. XII), метательных орудий (гл. XIII), лебедки (гл. XVI), клина, сводимого к двум рычагам (гл. XVIII), блока (гл. XIX), щипцов для вырывания зубов (гл. XXII), для орехов (гл. XXIII), колодезного рычажного подъемника (гл. XXIX) и др., короче говоря, все то, благодаря чему, по словам поэта Антифона, «берем искусством мы, где нас сильней природа». Все эти задачи решаются автором по приведенной выше схеме, поскольку «начало причинного объяснения всех подобных явлений заключается в круге» (847в15).

Для нас важно, однако, что эта техно-теоретическая схема полностью соответствует требованиям физико-теоретического анализа движения; исследование возможного движения сводится здесь к исследованию формы (машина как система связанных друг с другом рычагов, составляющих в потенции систему тех круговых траекторий, по которым вообще может совершаться данное движение, система, в которой машина функционирует,— форма-цель). Далее, динамика исследуется через кинематику, которая, в свою очередь, сводится к изучению состояния равновесия (возможного движения). Поэтому задачи теоретической механики, хотя и не вполне тождественны физическим, «но все же не будут целиком от них отличными; они представляют общий предмет как математических, так и физических исследований,— для них «каким образом» разъясняется математикой, а «почему» — физикой» (847а 25—30). Поскольку же рычаг является инструментом преобразования, с одной стороны, физической (естественной) силы в механическую (насильственную), с другой — естественного движения (вниз) в насильственное движение (по окружности) и, наконец, поскольку в нем «почему» (свойства круга) непосредственно связано с «каким образом» (форма перемещения), он и может рассматриваться как экспериментальное орудие в движении от механики к физике, которое, безусловно, гораздо менее явно выражено в греческой науке, чем движение противоположное.

По-видимому, нам удастся яснее представить «физическую» сущность закона рычага, если мы обратим внимание на его кинематический и динамический смысл, т. е. последовательно рассмотрим ту связь и превращение основных физических понятий, которые скрываются за простой геометрической формулировкой,— тем более, что «Механические проблемы» представляют нам такую возможность 46 .

У Аристотеля мы находим два принципа, которые позволяют сделать первые шаги на этом пути. Первый принцип связывает противоприродную силу 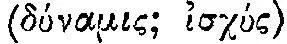, которая движет определенный груз 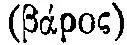, с величиной пути 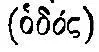, пройденного за определенное время 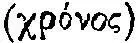. Мы уже говорили об этом динамическом законе, описанном в пятой главе VII книги «Физики» 47 . Фриц Крафт записывает его, используя греческие слова, которые нам в дальнейшем понадобятся, чтобы различить неразличимые в наших терминах понятия 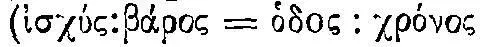48 ). В книге «О небе» этот закон выражен менее точно: «Если имеется некоторая сила 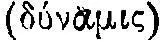, то же, что движимо, меньше и легче, то оно движется под действием той же силы больше. ...Причем скорость 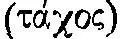меньшего так относится к скорости большего, как тело 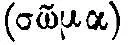большего относится к телу меньшего» 49 . (Слово 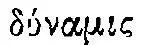означает мощность, потенцию, силу вообще, например, определенного человека, тогда как слово 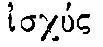означает конкретно действующую, приложенную силу).

Но у Аристотеля имеется принцип, согласно которому скорость естественного движения тела может быть выражена в геометрических параметрах. Рассматривая движение небесных тел, Аристотель замечает: «...Вполне разумно, что скорость больших кругов быстрее, если они <���круги> расположены вокруг одного и того же центра (концентрически),— а именно, как у других тел большее движется быстрее свойственным ему (естественным) движением, так же и у кругообразных <���то есть у концентрических эфирных сфер, для которых естественным является вращение вокруг центра мира). Ведь из двух отрезков, отсекаемых на круге линиями, исходящими из центра (отрезков дуг), больший находится на большем из кругов, потому что ясно, что больший круг обращается вокруг себя за то же самое время, что и малый» 50 . Последнее положение весьма важно, поскольку пути могут стать мерами скоростей только в том случае, если имеется независимая процедура, определяющая одновременность их прохождения. Но в системе связанных концентрических кругов угол поворота как раз и выполняет эту функцию единой меры времени. Тем более, что, как мы помним, вращение небес и было для Аристотеля моделью временной единицы, и именно благодаря тому, что единый угол поворота воплощал в себе единое время всех событий анизоциклического движения, линейная скорость была прямо пропорциональна (а при сравнениях эквивалентна) длинам описываемых дуг.