Георгий Гамов - Мистер Томпкинс внутри самого себя

— Производить вычисления в двоичной системе гораздо проще, — последовал ответ математика. — Более того, матушка-природа использует двоичную систему в том сложном компьютере, который вы называете своим головным мозгом. И нервные клетки, из которых состоит ваш мозг, и электронные лампы компьютеров могут находиться только в двух состояниях: возбужденном и невозбужденном. В обычном языке эти два состояния можно передать словами «да» или «нет», а в двоичной системе счисления — цифрами «1» или «0». Но с помощью этих двух состояний, передаваемых словами «да — нет» или «включено — выключено», можно построить всю логику и математику.

— Логику? — переспросил мистер Томпкинс. — Я думал, что компьютеры хороши только для вычислений, а логика относится исключительно к компетенции человека.

— Вы заблуждаетесь, — возразил молодой математик. —Арифметика и вся основанная на ней математика по праву считаются разделом логики. Поэтому компьютер вполне может справиться и с решением логических задач.

— А что вы имеете в виду под решением логических задач? — поинтересовался мистер Томпкинс. — Не могли бы вы привести какой-нибудь пример?

— Охотно. Возьмем хотя бы утверждение «Если будет стоять хорошая погода и светлое время суток, то полет состоится». Задача состоит в том, чтобы выяснить, состоится ли полет. Чтобы решить ее, необходимо «подставить» в утверждение информацию о погоде и времени суток, которой мы располагаем, и тогда утверждение скажет нам, состоится полет или не состоится. Это очень похоже на решение алгебраических уравнений, которому вас учили в школе. Например, пусть мы имеем уравнение

а + 2b = х

Если известно, что а = 2, b = 3, то х = 8. Аналогичным образом можно вычислить, чему равен х и при других значениях a и b. Логические задачи очень похожи на алгебраические за исключением того, что в них используется «двузначная логика», т. е. переменные могут принимать лишь одно из двух значений. В нашем примере погода может быть либо хорошей, либо плохой, время суток — либо светлым, либо темным, полет — либо состояться, либо не состояться. Поэтому логические вычисления даже проще арифметических, хотя, как я уже говорил, из логических отношений можно построить свою арифметику.

Дело в том, что все логические отношения можно свести к трем — «и», «или», «не», а их — реализовать с помощью простых электрических систем. Например, наше утверждение о полете можно записать следующим образом: (хорошая погода) и (светлое время суток) = (полет состоится). Из него следует, что не — (погода хорошая) и (светлое время суток) = не — (полет состоится) и т. д.

Предположим, что у нас имеется цепь, состоящая из батареи, лампы и двух реле.

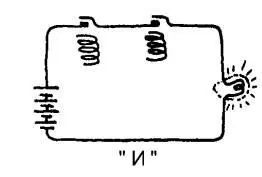
Если лампа горит, то это означает, что событие, в данном случае полет, состоится. Первое реле означает, не — (хорошая погода), т.е. погода не хорошая, если оно разомкнуто, и (хорошая погода), если оно замкнуто. Лампа загорится, т. е. «полет состоится», при условии, что оба реле замкнуты. Мы имеем в данном случае простую цепь «и».

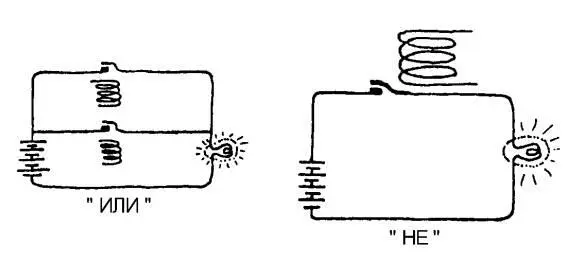
Рассмотрим теперь отношение «или»: «Если пилот Смит или пилот Джонс готовы к полету, то полет состоится». Цепь «или» имеет следующий вид:

Лампа загорится, если замкнуты любое из реле или оба.

Если вам нужна специальная цепь «не», то можете воспользоваться реле, которое нормально замкнуто и размыкается, только когда по обмотке соленоида идет ток: размыкание цепи и означает отрицание

Если мы хотим построить более сложные цепи, то ток вместо того чтобы подводить к зажимам лампы, следует подать на обмотку соленоида, управляющего другими цепями. Таким образом, если считать, что решение логических задач относится к мыслительной деятельности, то наши компьютеры мыслят.

— Должен признаться, что мне довольно трудно мыслить о мышлении в таких необычных терминах, — заметил мистер Томпкинс. — К тому же наш мозг состоит из нервных клеток, а не реле. Как он решает логические задачи?

— Прежде чем ответить на ваш вопрос, позволю себе обратить ваше внимание на то, что во многих случаях нервные клетки, или, как мы их обычно называем, нейроны, связаны между собой так, что образуют конфигурации, эквивалентные реле. Как вы, возможно, знаете, нейроны контактируют друг с другом через синапсы, в которых вещество, выделяемое одним нейроном, возбуждает следующий нейрон.

— Знаю, — кивнул мистер Томпкинс, — Это мне объяснил Сент.

— Тем лучше! Но коль скоро у вас имеется нейрон, связанный через синапс с другим нейроном, у вас имеется контакт, способный проводить импульсы. Предположим, что у вас имеются два входных нейрона, ведущих к одному и тому же синапсу. В этом случае вы получаете цепь «или»: импульс пройдет, если, либо один, либо другой из двух входных нейронов возбудится. Может представиться случай, когда синапс окажется устроенным так, что количество вещества, выделяемого один входным нейроном на синапсе окажется недостаточным для прохождения импульса и синапс «откроется» только при одновременном возбуждении двух входных нейронов. В этом случае вы получите цепь «и»: импульс проходит, если один и другой нейрон возбуждаются одновременно.

— Гм. А как вы получите цепь «не»?

— Некоторые нейроны выделяют вещества — ингибиторы, замедляющие протекание химических реакций; если один из таких нейронов возбужден, то он препятствует прохождению импульса через синапс.

Это можно рассматривать как логический эквивалент отрицания «не».

— Если я вас правильно понял, то наш мозг есть не что иное, как система взаимосвязанных реле, выполняющих логические операции?

Звучит просто.

— Не так просто, как вам кажется, — возразил математик. —

В действительности здесь много сложностей. Упомяну лишь одну из них. Нервные клетки вне головного мозга выглядят, как проволочки, или проводники, идущие к различным точкам тела. Но внутри головного мозга многие, в действительности большинство нейронов имеют гораздо более сложную форму — нечто вроде осьминога с бесчисленным количеством щупалец.

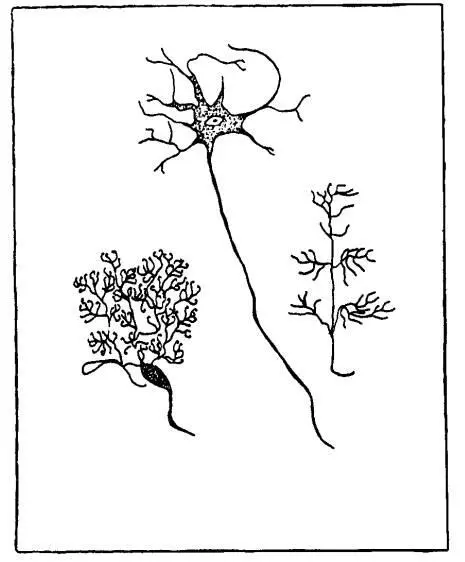
Большинство нервных клеток по виду напоминают осьминога с бесчисленным количеством щупалец.

Эти щупальцы образуют многочисленные синапсы как с щупальцами, отходящими от других нейронов, так и с щупальцами своей собственной клетки. Из-за сложности сети щупалец мы не знаем, ни как нейроны передают сигналы, ни о чем они сигнализируют. Очень часто, глядя на человеческий мозг, я не перестаю удивляться, как мы вообще можем мыслить. Но по крайней мере в отдельных случаях мы заведомо можем мыслить.