Георгий Гамов - Мистер Томпкинс внутри самого себя

Если же доминирует правое полушарие, то мы, естественно, получаем «левшу». Этим, в частности, объясняется, почему ребенок-левша, которого в школе заставляют переучиваться делать все правой рукой, часто становится заикой, у него развиваются и другие дефекты речи, он с трудом пишет и читает. Дело в том, что когда левшу заставляют все делать правой рукой, в его левом полушарии активизируются спавшие до того центры и начинают взаимодействовать с центрами правого полушария, которые были активными с самого начала. Когда же приказы поступают из двух центров, легко может возникнуть путаница.

— Не похоже ли то, о чем вы говорите, на конфликтующие приказы, которые могут отдавать отцовские и материнские хромосомы в клетках потомства? — спросил мистер Томпкинс.

— Никогда не слыхивал ни о чем подобном, — проскрежетал Маниак, и мистер Томпкинс понял, что несмотря на феноменальные способности в одной очень узкой области, робот был полной невеждой в большинстве остальных областей.

— Но мне не совсем понятно, как вы рассуждаете и решаете очень сложные математические задачи, — схитрил мистер Томпкинс, пытаясь вернуть беседу к теме, более знакомой Маниаку. — Не могли бы вы рассказать мне об этом более подробно?

— Конечно, могу, — ответил Маниак, и в голосе его прозвучали нотки нескрываемого превосходства, — но обещайте мне, что не станете возражать, если я буду говорить с вами несколько свысока.

— Обещаю, — заверил его мистер Томпкинс.

— Видите ли, — заговорил Маниак тоном заправского лектора, — когда мне задают задачу, я прежде всего читаю команды и запоминаю, как и что следует сделать для этого. Разумеется, команды должны быть записаны на машинном языке, или, как принято говорить «закодированы». Я произвожу вычисления, запоминаю промежуточные результаты, а когда дохожу до окончательного ответа, записываю его и останавливаюсь.

— Вот например, — продолжал Маниак, извлекая из корзины для использованных бумаг кусок бумажной ленты с длинными рядами пробитых в ней дырочек, — задача, которую задали мне вчера, желая продемонстрировать мои способности каким-то важным гостям. Меня попросили решить квадратное уравнение

15х2 + 137х = 4372,

или в двоичной системе

1111х2 + 10001001х = 1000100010100.

Как вы, должно быть, помните со школьной скамьи, существует особая формула для решения столь простого уравнения. У меня эта формула вместе с множеством других формул и таблицами хранится в специальном разделе моей памяти — так сказать, в моей информационной библиотеке.

Однако вчера от меня потребовали решить уравнение, не пользуясь готовой формулой, а с помощью последовательных приближений: я должен был подставлять вместо х значения 1, 2, 3 и т. д. до тех пор, пока не будут получены правильные значения корней уравнения. Команды для решения задачи «трудным путем» выглядели примерно так:

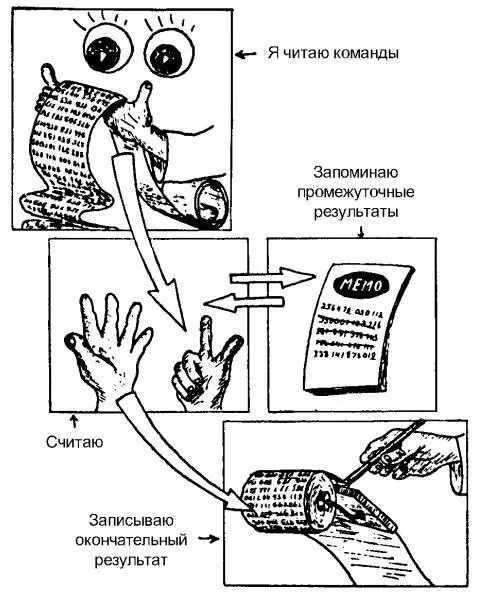
Для простоты числа представлены в десятичной, а не в двоичной системе

а) Запомнить число 1111.

б) Запомнить число 100001001.

в) Запомнить число 1000100010100.

г) Запомнить число 1.

д) Умножить четвертое число на себя.

е) Умножить полученный результат на первое число,

ж) Напомнить полученный результат.

з) Умножить четвертое число на второе

и) Прибавить полученное произведение к предыдущему результату.

к) Сравнить сумму с третьим числом.

л) Если сумма меньше третьего числа, то взять четвертое число и прибавить к нему 1.

м) Забыть (или стереть) старое четвертое число и запомнить вместо него новое.

н) Повторить все операции с самого начала, используя новое значение четвертого числа.

о) Когда результат станет больше третьего числа, запомнить его и перейти к следующей команде.

п) Вписать 1 в следующий разряд четвертого числа.

р) Умножить и т. д.

Команды были совершенно ясными, и я приступил к решению задачи. Я умножил 1 на 1, получил 1 и, умножив 1 на первое число, получил 1111. Записав это число в своей памяти, я умножил 10001001 на 1 и получил 10001001. Прибавив это число к ранее полученному результату, я получил число 10011000, которое меньше третьего числа (его, равное 1000100010100, я хранил в своей памяти). Следуя командам, я прибавил 1 к четвертому числу (также равному 1) и получил 2.

Используя 2 вместо 1 и умножив число 2 на себя, а затем на 1111, я получил 111100 ... Не буду докучать вам всеми деталями моих вычислений. Скажу лишь одно: когда четвертое число было 1101, или на привычном вам языке 13, результат все еще был меньше третьего числа, которое я по-прежнему хранил в своей памяти. Но стоило мне взять х равным 1110 (или 14), как результат стал слишком большим. Ясно, что корень уравнения заключен между 13 и 14.

— А более точное значение корня вы могли указать? —поинтересовался мистер Томпкинс.

— Конечно, мог. Получив первый результат и следуя дальнейшим командам, я начал пробовать числа, заключенные между 13,1 и 13,9.

Обнаружив, что правильный ответ лежит между 13,1 и 13,2, я попробовал придавать х значения, заключенные между 13,11 и 13,19. Так, шаг за шагом, я пришел к правильному решению — значению корня с 40 двоичными, или 12 десятичными, знаками.

— А сколько времени ушло у вас на вычисления? — спросил мистер Томпкинс с профессиональным интересом.

— Давайте прикинем. Мне пришлось выполнить около пятисот умножений и сколько-то сложений, которые требуют значительно меньше затрат времени. На одну операцию умножения мне приходится затрачивать одну миллисекунду, или 1/1000 секунды, т. е. для получения окончательного ответа — около половины секунды. Прошу вас иметь в виду, что все операции умножения я выполнил бы так же быстро и в том случае, если бы все коэффициенты уравнения были заданы с 12 знаками в десятичной системе. Иначе говоря, чтобы умножить 2 на 2, мне требуется столько же времени, сколько для умножения 275 036 289 706 на 573 024 696 271, поскольку и в том, и в другом случае мне приходится просматривать весь регистр, чтобы удостовериться, что других цифр нет. Решать простые задачи на электронных компьютерах невыгодно, так как на кодирование задачи у моих помощников уходит гораздо больше времени, чем у меня на решение.

— А вам случается ошибаться? — поинтересовался мистер Томпкинс.

— Ничто в мире не совершенно, — спокойно признал Маниак. — Если вы проводите сложные математические вычисления таким же способом как я, то все операции вы сводите к арифметическим, т.е. к сложению, вычитанию, умножению и делению. Но при таком подходе к решению задачи число операций, которые вам придется проделать, становится очень большим, как вы могли понять из приведенного выше примера. Используя обычную алгебраическую формулу, вы могли бы найти корень квадратного уравнения за какие-нибудь 10 операций, а тем способом, который был изложен выше, мне потребовалось более 500 операций. Мой способ, как принято говорить, имеет большую арифметическую глубину. Поскольку число элементарных шагов очень велико, сильно увеличивается вероятность совершения ошибки, которая может свести на нет ценность окончательного результата. Поэтому те, кто проектировал меня, стремились сделать вероятность возможной ошибки как можно более малой, значительно меньшей, чем вы могли бы счесть необходимым.