Ричард Фейнман - Том 1. Механика, излучение и теплота

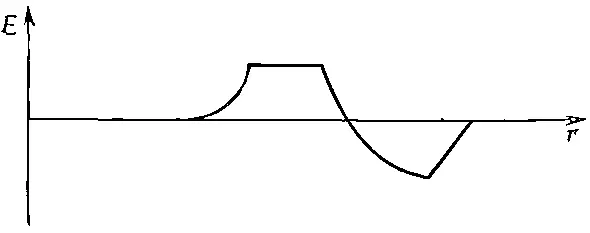
Фиг. 29.2. Ускорение некоторого заряда как функция времени.

Затем, чуть позже, измерим поле в разных точках пространства. Мы можем утверждать, что поле будет иметь вид, приведенный на фиг. 29.3.

Фиг. 29.3. Электрическое поле как функция положения точки наблюдения спустя некоторый промежуток времени. Множителем 1/r пренебрегаем.

В самом деле, поле в каждой точке определяется ускорением заряда в предыдущий момент времени, причем под словом «предыдущий» понимается r/ с секунд назад. Чем дальше точка, тем более ранним моментом времени определяется для нее ускорение. Поэтому кривая на фиг. 29.3 в некотором смысле есть «обращенный» во времени график ускорения; время и расстояние отличаются постоянным множителем c, который часто выбирается равным единице. Этот факт легко заметить и в математической записи a(t-r/с). Ясно, что добавка интервала времени Δt и вычитание отрезка пути Δr=-cΔt дают одну и ту же величину a(t-r/с).

Другими словами, увеличив время на Δt, можно восстановить значение a(t-r/с) добавлением отрезка Δr=сΔt, т. е. поле распространяется со временем как волна, уходящая от источника . Вот почему иногда говорят, что свет движется как волна. Можно также сказать, что поле запаздывает во времени, или иначе, что поле распространяется вширь с течением времени.

Особый интерес представляет случай периодических колебаний заряда q. В опыте, рассмотренном в гл. 28, смещение зарядов x в момент t равнялось некоторой константе х 0, амплитуде колебаний, умноженной на cosωt. Ускорение в этом случае равно

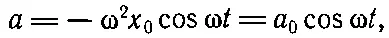(29.2)

где a 0, равное — ω 2 x 0, и есть амплитуда ускорения. Подставляя эту формулу в (29.1), находим

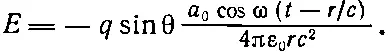(29.3)

Отвлечемся пока от угла θ и постоянных и посмотрим, как ведет себя Е (29.3) в зависимости от времени или координат.

Как мы уже говорили, в любой момент времени и в любой точке пространства напряженность поля меняется обратно пропорционально расстоянию r. Следует заметить, что энергия , несомая волной, и любые энергетические характеристики электрического поля пропорциональны квадрату поля. Пусть, например, заряд или осциллятор находится в электрическом поле и под влиянием поля начинает двигаться. Для линейного осциллятора смещение, ускорение и скорость, возникающие под действием поля, прямо пропорциональны величине поля. Поэтому кинетическая энергия заряда пропорциональна квадрату поля. Мы примем, что энергия, которую поле может передать какой-либо системе, пропорциональна квадрату поля.

Отсюда следует, что энергия, получаемая в данном месте от источника поля, уменьшается по мере удаления от источника, точнее, она падает обратно пропорционально квадрату расстояния. Существует очень простая интерпретация этого факта: соберем энергию волны, попадающую в конус с вершиной в источнике, сначала на расстоянии r1 (фиг. 29.4), а затем на расстоянии r 2; тогда количество энергии, падающее на единичную площадку, обратно пропорционально квадрату расстояния r, а площадь поверхности внутри конуса растет прямо пропорционально квадрату расстояния r от поверхности до вершины конуса.

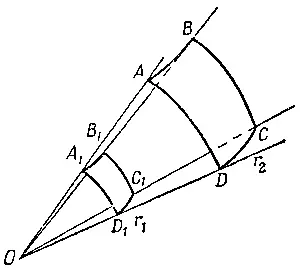
Фиг. 29.4. Количество энергии, протекающей внутри конуса OABCD, не зависит от расстояния r, на котором оно измеряется.

Таким образом, на каком бы расстоянии от вершины конуса мы ни находились, энергия, проходящая внутри конуса, одна и та же! В частности, если окружить источник со всех сторон поглощающими осцилляторами, то полное количество энергии, поступающее в них от волны, будет постоянным, независимо от расстояния до источника. Закон спадания поля Е как 1/r эквивалентен утверждению, что имеется поток энергии, который нигде не теряется; при этом энергия распространяется на все большие и большие области пространства. Таким образом, заряд, колеблясь, безвозвратно теряет энергию, уходящую все дальше и дальше. Заряд не может вернуть излученную энергию с тех расстояний, где применимо наше рассмотрение; для достаточно больших расстояний от источника вся излученная энергия уходит прочь. Конечно, энергия не исчезает бесследно и ее можно поглотить с помощью других систем. Потери энергии на излучение мы будем изучать в гл. 32.

Рассмотрим теперь более подробно волны вида (29.3) как функции времени в данном месте и как функции расстояния в данный момент времени. Как и раньше, будем отвлекаться от постоянных множителей и множителя 1/r.

Зафиксируем вначале r и рассмотрим поле как функцию времени. Получается функция, которая осциллирует с угловой частотой ω. Угловую частоту со можно определить как скорость изменения фазы со временем (радианы в секунду). Эта величина нам уже знакома. Период есть время одного колебания, одного полного цикла; он равен 2π/ω, так как произведение ω и периода есть полный период косинуса.

Введем новую величину, которая очень часто используется в физике. Она возникает в другой ситуации, когда t фиксировано и волна рассматривается как функция расстояния r. Легко увидеть, что как функция r волна (29.3) тоже осциллирует. Если отвлечься от множителя 1/r, то мы видим, что Е тоже осциллирует, когда мы меняем положение. Тогда по аналогии с ω введем так называемое волновое число и обозначим его через k. Оно определяется как скорость изменения фазы с расстоянием (радианы на метр). Время при таком изменении остается фиксированным.

Роль периода здесь играет другая величина, ее можно было бы назвать периодом в пространстве, однако ее обычное название — длина волны, а обозначается она буквой λ. Длина волны есть расстояние, на котором колебание поля совершает один полный цикл. Легко видеть, что длина волны равна 2π/k, потому что k , умноженное на длину волны, равно полному периоду косинуса. Итак, соотношение kλ=2π полностью аналогично ωt 0=2π.

В нашем конкретном случае между частотой и длиной волны имеется определенная связь, однако приведенные выше определения k и ω носят совершенно общий характер и применимы также в тех физических условиях, когда никакого соотношения между этими величинами нет. Для рассматриваемой нами волны скорость изменения фазы с расстоянием найти легко. В самом деле, запишем выражение для фазы φ=ω(t-r/с) и возьмем частную производную по r