Ричард Фейнман - Том 1. Механика, излучение и теплота

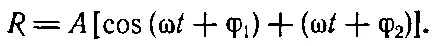(29.9)

На уроках тригонометрии вы, вероятно, доказывали равенство

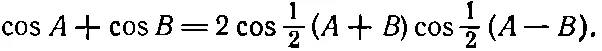(29.10)

Если это нам известно, то мы немедленно получаем R:

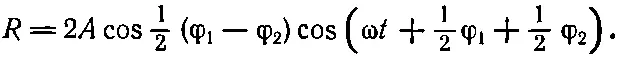(29.11)

Итак, мы снова получили синусоидальную волну, но с новой фазой и новой амплитудой. Вообще результат сложения двух синусоидальных волн есть синусоидальная волна с новой амплитудой A R , называемой результирующей амплитудой, и новой фазой φ R, называемой результирующей фазой. В нашем частном случае результирующая амплитуда равна

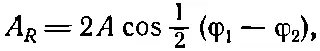(29.12)

а результирующая фаза есть арифметическое среднее обеих фаз. Таким образом, поставленная задача полностью решена. Предположим теперь, что мы забыли формулу сложения косинусов. Тогда можно применить другой метод решения — геометрический. Косинус, зависящий от ωt, можно представить в виде горизонтальной проекции некоторого вращающегося вектора . Пусть имеется вектор А 1, вращающийся с течением времени; длина его равна A 1, а угол с осью абсцисс равен ωt+φ 1. (Мы пока опустим слагаемое ω t ; как мы увидим, при выводе это не играет роли.) Сделаем моментальный снимок векторов в момент времени t =0, помня, что на самом деле вся схема вращается с угловой скоростью ω (фиг. 29.9).

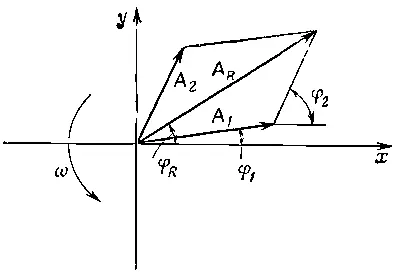
Фиг. 29.9. Геометрический способ сложения двух косинусоидальных волн. Чертеж вращается со скоростью ω против часовой стрелки.

Проекция A 1на ось абсцисс в точности равна A 1cos(ωt+φ 1). В момент времени t=0 вторая волна представляется вектором A 2, длина которого равна A 2, а его угол с осью абсцисс равен φ 2, причем он тоже вращается с течением времени. Оба вектора вращаются с одинаковой угловой скоростью ω, и их относительное расположение неизменно. Вся система вращается жестко, подобно твердому телу.

Горизонтальная проекция А 2равна A 2 cos (ω t +φ 2). Из векторного анализа известно, что при сложении двух векторов по правилу параллелограмма образуется новый, результирующий вектор А R, причем x-компонента его есть сумма х-компонент слагающих векторов. Отсюда получаем решение нашей задачи. Легко проверить, что получается правильный ответ в нашем частном случае A 1= А 2= А . Действительно, из фиг. 29.9 очевидно, что A R лежит посредине между A 1и А 2и составляет угол 1/2(φ 2-φ 1) с каждым из них. Следовательно, A R =2 А cos 1/ 2(φ 2-φ 1), что совпадает с прежним результатом. Кроме того, в случае А 1- А 2фаза A Rесть среднее от фаз A 1и А 2. Для неравных A 1и А 2задача решается столь же просто. Мы можем назвать это геометрическим решением задачи.

Существует еще один метод решения задачи, его можно было бы назвать аналитическим . Вместо того чтобы рисовать схему, подобную приведенной на фиг. 29.9, напишем выражения, имеющие тот же смысл, что и чертеж, и сопоставим каждому вектору комплексное число . Действительные части этих комплексных чисел отвечают реальным физическим величинам. В нашем конкретном случае волны записываются следующим образом: A 1ехр[i(ωt+φ 1)] [действительная часть этого равна A 1cos(ωt+φ 1)] и A 2ехр[i(ωt-+φ 2)]. Сложим обе волны:

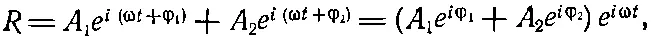(29.13)

или

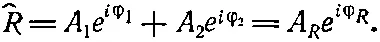(29.14)

Задача, таким образом, решена, так как мы имеем окончательный результат в виде комплексного числа с модулем A Rи фазой φ R.

Для иллюстрации аналитического метода найдем амплитуду А R, т. е. «длину» R . «Длина» комплексного числа в квадрате есть само комплексное число, умноженное на сопряженное ему.

Комплексное сопряжение состоит в изменении знака i. Отсюда получаем

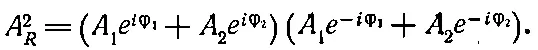(29.15)

Перемножая, получаем A 1 2+A 2 2и перекрестные члены

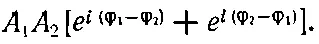
Далее

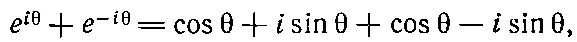
т. e. e i θ+ e - i θ=2cosθ. Следовательно, окончательный результат есть

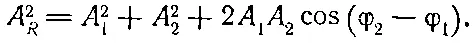(29.16)

(С помощью формул тригонометрии легко установить совпадение получаемого результата с длиной A Rна фиг. 29.9.)

Итак, суммарная интенсивность складывается из члена А 1 2, возникающего от действия только первого источника, интенсивности А 2 2, равной интенсивности второго источника, и еще дополнительного члена. Этот дополнительный член мы назовем эффектом интерференции . Он представляет собой разность между истинным результатом сложения и суммой интенсивностей. Интерференционный член может быть как положительным, так и отрицательным. [Интерференция (interference) в английской разговорной речи означает возражение, помеху, но в физике слова часто теряют первоначальный смысл и употребляются совсем в другом значении!] Если интерференционный член положителен, мы будем говорить о конструктивной интерференции (буквальный смысл этого выражения покажется ужасным всем, кроме физиков!). В противном случае мы говорим о деструктивной интерференции.

Посмотрим теперь, как применить нашу общую формулу (29.16) для сложения полей излучения двух осцилляторов к тем частным случаям, которые мы уже качественно обсуждали. Для этого необходимо лишь вычислить разность фаз φ 1-φ 2двух сигналов, приходящих в данную точку пространства. (Эффект, разумеется, связан с разностью фаз, а не с их абсолютными значениями.) Рассмотрим случай, когда два осциллятора с равными амплитудами и с относительной фазой колебаний α (когда колебания одного имеют фазу нуль, фаза другого равна α) расположены на расстоянии d друг от друга. Будем искать интенсивность под углом θ к линии запад — восток. [Заметьте, что этот угол не имеет ничего общего с углом θ в формуле (29.1).] Разность расстояний от точки Р до осцилляторов равна dsinθ (фиг. 29.10), поэтому разность фаз, возникающая по этой причине, равна числу длин волн, заключенных на отрезке d sinθ, умноженному на 2π.