Ричард Фейнман - Том 1. Механика, излучение и теплота

Подставляя φ=3π/n, получаем sin 23π/2=1 в числителе (30.3) (с этой целью и был выбран угол φ) и sin 23n/2n в знаменателе. Для достаточно большого n можно заменить синус его аргументом: sin 3π/2n=3π/2n. Отсюда интенсивность во втором максимуме оказывается равной I=I 0(4n 2/9π 2). Но n 2I 0— не что иное, как интенсивность в первом максимуме, т. е. интенсивность второго максимума получается равной 4/9π 2от максимальной, что составляет 0,047, или меньше 5%! Остальные максимумы, очевидно, будут еще меньше. Таким образом, возникает очень узкий основной максимум и очень слабые дополнительные максимумы по обе стороны от основного.

Можно показать, что площадь под кривой интенсивности, включая все максимумы, равна 2πnI 0и в два раза превышает площадь пунктирного прямоугольника на фиг. 30.2.

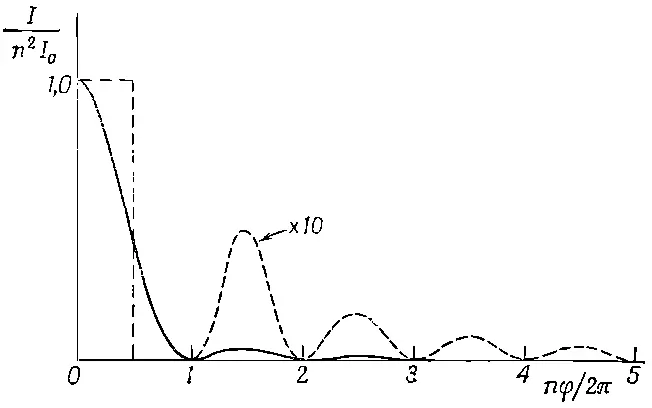
Фиг. 30.2. Зависимость интенсивности от фазового угла для большого числа осцилляторов с одинаковыми амплитудами.

Посмотрим теперь, что дает формула (30.3) в приложении к разным случаям. Пусть источники расположены на одной линии, как показано на фиг. 30.3.

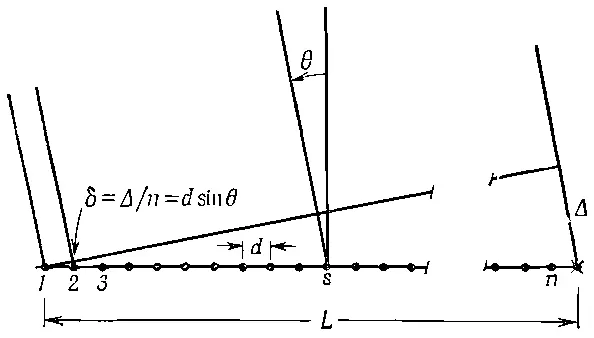
Фиг. 30.3. Устройство из n одинаковых осцилляторов, расположенных на линии. Фаза колебания s-го осциллятора равна a s =sa.

Всего имеется n источников на расстоянии d друг от друга, и сдвиг фазы между соседними источниками выбран равным α. Тогда для лучей, распространяющихся в заданном направлении θ, отсчитываемом от нормали, вследствие разности хода лучей от двух соседних источников возникает дополнительный сдвиг фазы 2πd(1/λ)sinθ. Таким образом,

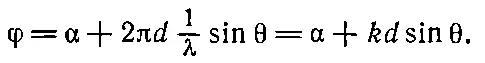(30.4)

Рассмотрим сначала случай α=0. Все осцилляторы колеблются с одной фазой; требуется найти интенсивность их излучения как функцию угла θ. Подставим с этой целью φ= kdsin θ в формулу (30.3) и посмотрим, что получится в результате. Прежде всего при φ=0 возникает максимум. Значит, осцилляторы, колеблющиеся с одной фазой, дают мощное излучение в направлении θ=0. Интересно узнать, где находится первый минимум.

Он возникает при φ=2π/n; другими словами, первый минимум кривой интенсивности определяется из соотношения (2πd/λ)sinθ=2π/ n . Сокращая на 2π, получаем

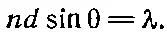(30.5)

Теперь разберем с физической точки зрения, почему минимум возникает именно в этом месте. В этом выражении nd есть полная длина L нашей системы осцилляторов. Обращаясь к фиг. 30.3, мы видим, что ndsinθ= L sinθ=Δ. Формула (30.5) подсказывает нам, что минимум возникает при Δ, равном одной длине волны . Но почему минимум получается при Δ=λ? Дело в том, что поля от отдельных осцилляторов равномерно распределены по фазе от 0 до 360°. Стрелки (см. фиг. 30.1) описывают полную окружность; мы складываем равные векторы, имеющие произвольные направления, а в этом случае сумма равна нулю. Вот при таких значениях угла, когда Δ=λ, возникает минимум. Это и есть первый минимум.

Формула (30.3) имеет еще одну важную особенность: при увеличении угла φ на число, кратное 2π, значение интенсивности не меняется. Поэтому для φ=2π, 4π, 6π и т. д. также возникают резкие и высокие максимумы. Вблизи этих максимумов интенсивность повторяет свой ход (см. фиг. 30.2). Зададимся вопросом, в силу каких геометрических соотношений возникают другие максимумы? Условие появления максимума записывается в виде φ=2πm, где m — любое целое число. Отсюда получаем (2πd/λ)sinθ=2πm. Сокращая на 2π, получаем

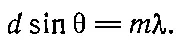(30.6)

Это соотношение очень похоже на формулу (30.5). Однако там было nd sin θ=λ. Разница в том, что здесь нужно взять каждый отдельный источник и выяснить, что для него означает условие dsin θ= m λ; угол θ здесь таков, что разность хода δ= m λ. Другими словами, волны, идущие от источников, различаются по фазе на величину, кратную 360°, и, следовательно, все находятся в фазе . Поэтому при сложении волн возникает столь же высокий максимум, как и в рассмотренном ранее случае m =0. Побочные максимумы и весь ход интенсивности здесь такие же, как в случае φ=0. Таким образом, наша система посылает пучки лучей в разных направлениях, причем каждый пучок имеет высокий центральный максимум и ряд слабых боковых. Главные (центральные) максимумы в зависимости от величины m называются максимумами нулевого, первого и т. д. порядков; m называют порядком максимума.

Обратите внимание на такой факт: если d меньше λ, то формула (30.6) имеет единственное решение при m =0. Поэтому для малого расстояния между источниками возникает один-единственный пучок, сконцентрированный около θ=0. (Разумеется, есть еще пучок в обратном направлении.) Чтобы получить максимумы других порядков, расстояние d должно быть больше одной длины волны.

На практике равенство фаз осцилляторов или антенн достигается с помощью проводов и всяких специальных устройств. Возникает вопрос, можно ли и как создать подобную систему для света. Сейчас мы еще не умеем делать маленькие радиостанции оптической частоты в буквальном смысле слова, соединять их крохотными проволочками и устанавливать для всех них одинаковые фазы. Однако есть другой очень простой способ, позволяющий добиться этой цели.

Предположим, у нас имеется большое количество параллельных проводов, отстоящих друг от друга на расстоянии d, и источник радиоволн, расположенный очень далеко, практически на бесконечности. Этот источник создает электрическое поле у каждой из проволочек с одной и той же фазой. (Можно взять и объемную систему проводов, но мы ограничимся плоской системой.) Тогда внешнее электрическое поле будет двигать электроны взад и вперед в каждой проволочке, в результате они становятся новыми излучателями . Такое явление называется рассеянием : свет от некоторого источника вызывает движение электронов в среде, а оно в свою очередь генерирует собственные волны. Поэтому достаточно взять ряд проволок на равном расстоянии друг от друга, подействовать на них радиоволнами от удаленного источника, и получается нужная нам система без всяких специальных контуров и т. п. Если лучи падают по нормали к плоскости проводов, фазы колебаний будут одинаковыми и возникнет та картина, о которой говорилось выше. Так, при расстоянии между проволочками, превышающем длину волны, максимальная интенсивность рассеяния получается в направлении нормали и в других направлениях, определяемых формулой (30.6.).