Ричард Фейнман - Том 1. Механика, излучение и теплота

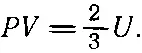(39.10)

Немного задержимся и ответим на такой вопрос: предположим, что мы медленно сжимаем газ; каким должно быть давление, чтобы сжать газ до заданного объема? Определить это легко, так как давление есть энергия, деленная на объем. Но когда газ сжимается, производится работа и поэтому энергия газа U возрастает. Процесс сжатия описывается неким дифференциальным уравнением. В начальный момент газ занимает определенный объем и обладает определенной энергией, поэтому нам известно и давление. Как только мы начинаем сжимать газ, энергия U возрастает, объем V уменьшается, а как изменяется давление, нам еще предстоит узнать.

Итак, нам предстоит решить дифференциальное уравнение. Сейчас мы это сделаем. Однако подчеркнем сначала, что, сжимая газ, мы предполагаем, что вся работа уходит на увеличение энергии атомов газа. Вы спросите: «А необходимо ли на этом останавливаться? Куда же еще она может уйти?» Но оказывается, что затраченная работа может уйти и в другое место. Энергия может «вытечь» из ящика сквозь стенки: горячие (т. е. очень быстрые) атомы при бомбардировке будут нагревать стенки ящика и энергия выйдет наружу. Но мы предполагаем, что в нашем случае этого не происходит.

Сделаем небольшое обобщение, хотя и в этом случае мы будем рассматривать лишь очень частный случай: запишем вместо PV = 2/ 3 U

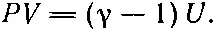(39.11)

Энергия U умножается на (γ-1) для удобства, потому что в дальнейшем нам придется иметь дело с газами, для которых множитель перед U равен не 2/ 3, а какому-то другому числу. Чтобы можно было описывать и такие случаи, запишем этот множитель так, как его обозначают почти сто лет. Тогда в нашем случае одноатомного газа, такого, как гелий, γ= 5/ 3, потому что 5/ 3-1= 2/ 3.

Мы уже говорили, что совершаемая при сжатии газа работа равна - PdV . Сжатие, при котором тепло не поглощается и не выделяется, называется адиабатическим сжатием; это слово образовано из трех греческих слов: а(не)+dia(сквозь)+bainein(проходить). (Слово адиабатический употребляется в физике в разных смыслах, так что не всегда можно понять, что между ними общего.) При адиабатическом сжатии вся затраченная работа уходит на изменение внутренней энергии. Вот в этом и смысл, что нет потерь энергии и, значит, PdV =- dU . Но поскольку U=PV/γ-1, то можно записать

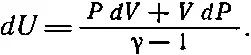(39.12)

Итак, PdV=-(PdV+VdP)/(γ-1) или, приводя подобные члены, получаем γPdV=-VdP, или

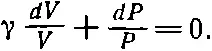(39.1З)

Если мы примем, что γ постоянна, а это так в случае одноатомных газов, то уравнение интегрируется и мы получаем γlnV+ lnP =lnC, где С — постоянная интегрирования. Переходя к степеням, мы получаем такой закон:

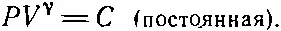(39.14)

Иначе говоря, если выполнены условия адиабатичности, т. е. потерь энергии нет и газ при сжатии нагревается, то в случае одноатомного газа произведение объема на давление в степени 5/ 3есть величина постоянная! Этот результат мы получили чисто теоретически, но опыт показывает, что и в действительности все происходит именно так.

Приведем еще один пример из кинетической теории газов; он не особенно интересует химиков, но очень важен для астрономов. Внутри нагретого до высокой температуры ящика имеется огромное число фотонов. (В качестве такого ящика надо взять очень горячую звезду. Солнце недостаточно горячо для этих целей. В звезде, правда, слишком много атомов, но если ее температура очень высока, то атомами можно пренебречь и считать, что внутренность звезды целиком заполнена фотонами.) Вспомним теперь, что фотон обладает импульсом р. (При изучении кинетической теории газов мы всегда будем испытывать страшные неудобства: P — это давление, но р— еще и импульс; V — это объем, но это и скорость одновременно, а Т — это и температура, и кинетическая энергия, и время, и момент силы; тут нужен глаз да глаз.) Сейчас буква р— это импульс, вектор. Поступим так же, как и в предыдущем параграфе, за удары фотонов о стенку ответственна x-составляющая импульса, а удвоенная x-составляющая импульса — это импульс, полученный стенкой после каждого удара. Итак, вместо 2 mv x пишем 2 р x , а при вычислении числа столкновений нужно по-прежнему подставлять v x ; проделав все это, формулу (39.4) для давления мы уже записываем в виде

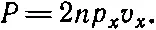(39.15)

После усреднения мы получим произведение n на среднее значение p x v x (вспомните, что мы говорили о множителе 2), а после того как на помощь будут призваны два других измерения, мы найдем

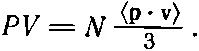(39.16)

Эта формула почти совпадает с (39.9), потому что импульс равен m v, просто это более общая формула, вот и все. Произведение давления на объем равно произведению полного числа атомов на среднее значение 1/ 3( p· v).

Чему равно p· vдля фотонов? Импульс и скорость направлены одинаково, а скорость равна скорости света, поэтому интересующее нас произведение — это импульс фотона, умноженный на скорость света. Произведение импульса фотона на скорость света — это энергия фотона: Е = рс . Мы имеем дело с энергией каждого фотона и должны умножить среднюю энергию фотона на число фотонов. Получается одна треть полной энергии:

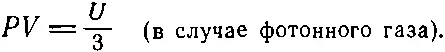(39.17)

Для фотонов, следовательно, поскольку впереди стоит 1/ 3, множитель (γ-1) в (39.11) равен 1/ 3, т . е. γ= 4/ 3, значит, излучение в ящике подчиняется закону

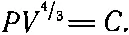(39.18)

Таким образом, мы знаем сжимаемость излучения! Можно использовать эту формулу при анализе вклада излучения в давление внутри звезды, подсчитать давление и оценить, как оно изменяется при сжатии звезды. Просто удивительно, как много мы уже умеем!