Ричард Фейнман - Том 1. Механика, излучение и теплота

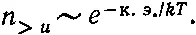(40.4)

Этот способ описания распределения по скоростям —когда подсчитывается число молекул, проходящих через выделенную площадку с заданной минимальной z-составляющей скорости,— отнюдь не самый удобный. Например, чаще хотят знать, сколько молекул в заданном объеме газа движется, имея z -составляющую скорости между двумя заданными значениями, а это, конечно, из (40.4) сразу не получишь. Поэтому придадим нашей формуле удобную форму, хотя то, что мы получили, — это весьма общий результат. Заметим, что невозможно утверждать, что любая молекула в точности обладает той или иной наперед заданной скоростью ; ни одна из них не движется со скоростью, в точности равной 1,7962899173 м / сек . Итак, чтобы придать нашему утверждению какой-то смысл, мы должны спросить, сколько молекул можно найти в заданном интервале скоростей. Нам придется говорить о том, как часто встречаются скорости в интервале между 1,796 и 1,797 и т. п. Выражаясь математически, пусть f ( u ) du будет долей всех молекул, чьи скорости заключены в промежутке u и u + du, или , что то же самое (если du бесконечно мало), долей всех молекул, имеющих скорость и с точностью до du . На фиг. 40.5 представлена возможная форма функции f(u), а заштрихованная часть ширины du и средней высоты f ( u ) — это доля молекул f ( u ) du .

Таким образом, отношение площади заштрихованного участка ко всей площади под кривой равно относительному числу молекул со скоростью и внутри отрезка du .

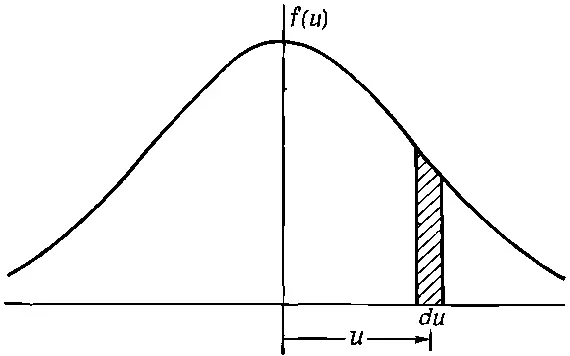
Фиг. 40.5. Функция, распределения скоростей. Заштрихованная площадь равна f(u)du — это относительное число частиц, скорости которых заключены внутри отрезка du около точки u.

Если определить f ( u ) так, что относительное число молекул будет просто равно площади заштрихованного участка, то полная площадь под кривой — это все 100% молекул, т. е.

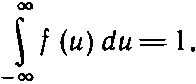(40.5)

Теперь остается только найти это распределение, сравнив его с результатом доказанной ранее теоремы. Сначала надо выяснить, как выразить через f ( u ) число молекул, проходящих за 1 сек через заданную площадку со скоростью, превышающей u?

Это число не равно интегралу u∫ ∞ f ( u ) du (хотя это первое, что приходит в голову), ведь нас интересует число молекул, проходящих через площадку за секунду . Более быстрые молекулы будут пересекать площадку, так сказать, чаще, чем более медленные, поэтому, чтобы найти число проходящих молекул, надо умножить плотность молекул на скорость. (Мы уже обсуждали это в предыдущей главе, когда подсчитывали число столкновений.)

Полное число молекул, проходящих через поверхность за время t , равно числу молекул, способных достигнуть поверхности, а это молекулы, проходящие к поверхности с расстояния ut . Таким образом, число молекул, достигающих площадки, определяется не просто числом молекул, движущихся с данной скоростью, а равно этому числу, отнесенному к единице объема, и умноженному на расстояние, которое они пройдут, прежде чем достигнут площадки, сквозь которую они, по-видимому, должны пройти, а это расстояние пропорционально u . Значит, нам предстоит вычислить интеграл от произведения и на f ( u ) du , взятый от u до бесконечности, причем мы уже знаем, что этот интеграл обязательно должен быть пропорционален ехр(- mu 2/2 kT ), а постоянную пропорциональности еще надо определить:

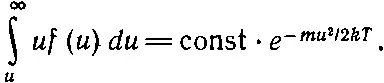(40.6)

Если теперь продифференцировать интеграл по u , то мы получим подынтегральное выражение (со знаком минус, потому что u — это нижний предел интегрирования), а дифференцируя правую часть равенства, мы получим произведение u на экспоненту (и на некоторую постоянную). Сократим в обеих частях и , и тогда

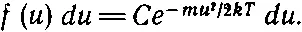(40.7)

Мы оставили в обеих частях равенства du , чтобы помнить, что это распределение ; оно говорит нам об относительном числе молекул, имеющих скорость между u и u + du .

Постоянная С должна определиться из условия равенства интеграла единице в согласии с уравнением (40.5). Можно доказать [31] Чтобы вычислить этот интеграл, положим Тогда а это двойной интеграл в xy-плоскости. Но его можно вычислить и в полярных координатах: , что

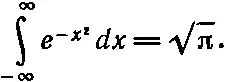
Используя это обстоятельство, легко найти С =√( m /2π kT ).

Поскольку скорость и импульс пропорциональны, можно утверждать, что распределение молекул по импульсам, отнесенное к единице импульсной шкалы, также пропорционально ехр(- к.э ./ kT ). Оказывается, что эта теорема верна также в теории относительности, если только формулировать ее в терминах импульсов, тогда как в терминах скоростей это уже не так; поэтому сформулируем все в терминах импульсов:

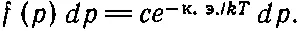(40.8)

Это значит, что мы установили, что вероятности, определяемые энергиями разного происхождения (и кинетической и потенциальной), в обоих случаях выражаются одинаково: ехр(-энергия/kT); таким образом, наша замечательная теорема приобрела форму, весьма удобную для запоминания.

Однако пока мы говорили только о «вертикальном» распределении скоростей. Но мы можем спросить, какова вероятность того, что молекула движется в другую сторону? Конечно, эти распределения связаны друг с другом и можно получить полное распределение, исходя из какого-то одного, ведь полное распределение зависит только от квадрата величины скорости, а не от ее z-составляющей. Распределение по скоростям не должно зависеть от направления и определяться только функцией u 2— вероятностью величины скорости. Нам известно распределение z-составляющей, и мы хотим получить отсюда распределение других составляющих. В результате полное распределение по-прежнему пропорционально ехр(-к.э./kT), только теперь кинетическая энергия состоит из трех частей: mv x 2/2, mv y 2/2 и mv z 2/2, суммируемых в показателе экспоненты. А можно записать это и в виде произведения: