Ричард Фейнман - Том 1. Механика, излучение и теплота

Заметим, что это два совершенно независимых вопроса и что распределение по скоростям всегда одинаково. Этого можно было ожидать после того, как мы выяснили, что средняя кинетическая энергия степени свободы всегда равна 1/ 2 kT , независимо от того, какие силы действуют на молекулы. Распределение по скоростям молекул не зависит от сил, потому что силы не влияют на частоту столкновений.

Давайте начнем с примера распределения молекул в атмосфере, подобной той, в которой мы живем, но без ветра или других каких-либо возмущений.

Предположим, что мы имеем дело с довольно высоким столбом газа, находящегося в тепловом равновесии (не так, как в настоящей атмосфере; в ней, как известно, по мере подъема вверх становится холоднее). Укажем здесь, что нарушение равновесия в случае разницы температур на разных высотах можно продемонстрировать, поместив в столб газа металлический стержень так, что его концы соприкасаются с маленькими шариками (фиг. 40.1).

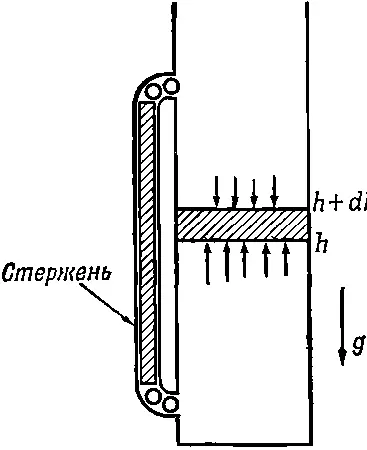
Фиг. 40.1. Равновесие в атмосфере с постоянной температурой. Давление на высоте h должно превосходить давление на высоте h+dh на вес заключенного между этими уровнями газа. Стержень и шарики выравнивают температуру.

Нижние шарики, получая от молекул газа энергию 1/ 2 kT , передают ее через стержень верхним шарикам и встряхивают их; верхние шарики в свою очередь будут встряхивать соприкасающиеся с ними наверху молекулы. В конце концов, конечно, температура на разных высотах гравитационного поля станет одинаковой.

Нам предстоит найти закон, по которому происходит разрежение атмосферы по мере подъема вверх, когда температура на всех высотах одинакова. Если N — полное число молекул в объеме V газа с давлением Р , то PV = NkT , или Р = nkT , где n — число молекул в единичном объеме. Иначе говоря, если известно число молекул в единичном объеме, то известно и давление, и наоборот: давление и плотность пропорциональны друг другу, ведь температура в нашем случае постоянна. Но давление не может быть постоянным: с уменьшением высоты оно должно возрастать, потому что нижнему слою приходится, так сказать, выдерживать вес всех расположенных сверху атомов. Теперь можно определить, как давление меняется с высотой. Если на высоте h выделить площадку единичной площади, то на эту площадку снизу будет действовать сила, равная давлению Р . Если бы не было силы тяжести, то на площадку на высоте h + dh действовала бы сверху вниз точно такая же сила. Но в нашем случае это не так: действующая снизу сила должна превосходить силу, действующую сверху, на величину, равную весу газа, заключенного между слоями h и h + dh . На каждую молекулу действует сила тяжести mg , где g — ускорение силы тяжести. В интересующем нас слое находится ndh молекул. Это приводит к такому дифференциальному уравнению: P h + dh - P h = dP =- mgndh . Поскольку Р = nkT, а Т — постоянная, то можно избавиться или от Р , или от n. Исключим из уравнений Р ; тогда получим

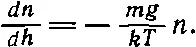
Это дифференциальное уравнение говорит нам, как убывает плотность по мере увеличения высоты.

Мы располагаем теперь дифференциальным уравнением для плотности частиц n, которая меняется с высотой, но меняется так, что производная плотности пропорциональна себе самой. Функция, производная которой пропорциональна себе самой,— это экспоненциальная функция и, значит, решение дифференциального уравнения имеет вид

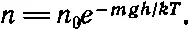(40.1)

Здесь постоянная интегрирования n 0— плотность на высоте h =0 (которую можно задать произвольно); с высотой плотность экспоненциально убывает.

Заметим, что если имеется несколько сортов молекул с разными массами, то число их убывает по разным экспонентам. Число более тяжелых молекул убывает с высотой быстрее, чем число легких молекул. Поэтому можно ожидать, что раз кислород тяжелее азота, то по мере подъема вверх относительное содержание азота в атмосфере (смеси азота и кислорода) будет возрастать. В нашей атмосфере, во всяком случае на доступных высотах, этого фактически не происходит, ибо вследствие воздушных возмущений газы вновь перемешиваются. Ведь это же не изотермическая атмосфера. Тем не менее на больших высотах преобладают очень легкие газы, например водород, так как молекулы легких газов способны забраться на такую высоту, где все остальные экспоненты уже вымрут (фиг. 40.2).

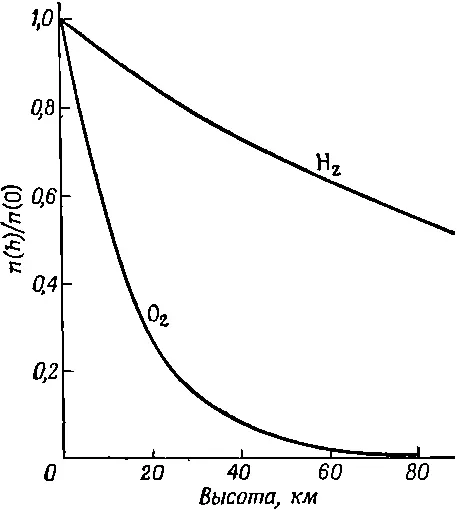
Фиг. 40.2. Нормированная плотность как функция высоты в гравитационном поле Земли для кислорода и водорода при постоянной температуре.

Отметим здесь тот факт, что числитель показателя экспоненты в равенстве (40.1) — это потенциальная энергия атома. Поэтому можно в нашем случае сформулировать закон следующим образом: плотность в каждой точке пропорциональна

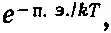
где п.э. — потенциальная энергия отдельного атома.

Возможно, что это случайность и этот закон справедлив только в частном случае однородного гравитационного поля. Однако можно показать, что это весьма общее утверждение. Предположим, что на молекулы газа действуют какие-то иные, не гравитационные, силы. Например, молекулы обладают электрическим зарядом, а тогда они реагируют на электрическое поле или на другой заряд, притягивающий их. А может быть, в результате взаимного притяжения атомов друг к другу или к стенкам, или к какому-нибудь твердому телу, или еще к чему-то существуют какие-то силы притяжения, которые зависят от взаимного расположения молекул и действуют на все молекулы. Предположим теперь для простоты, что все молекулы одинаковы и что сила действует на каждую отдельную молекулу, так что полная сила, действующая на произвольно выделяемую часть газа, равна просто произведению числа молекул на силу, действующую на одну молекулу. Дело совсем упростится, если выбрать систему координат так, что сила Fбудет действовать вдоль оси х .