Ричард Фейнман - Том 1. Механика, излучение и теплота

Сравнивая (45.3) и (45.8), мы убедимся, что уравнение для резины получилось сразу после замены одних букв другими. Если заменить V на L, а Р на — F , то все аргументы цикла Карно окажутся применимыми и к резине. Можно тотчас же, скажем, вывести, что нужное для растяжения на ΔL тепло Δ Q определяется уравнением, аналогичным (45.5): ΔQ=— Т (∂ F /∂ T ) L Δ L . Это уравнение говорит нам, насколько увеличится сила, если длина резиновой полоски при нагревании останется постоянной. Надо только узнать, сколько тепла требуется для поддержания постоянной температуры при небольшом растяжении полоски. Итак, мы видим, что и к резине, и к газу применимы одни и те же уравнения. Можно даже писать ΔU=ΔQ+AΔB, где А и В — самые разные величины, сила и длина, давление и объем и т. д. Если интересует поведение газа, нужно заменить A и В на Р и V .

Для примера рассмотрим разность электрических потенциалов, или электродвижущую силу (э. д. с.) батареи Е , и заряд ΔZ, прошедший через батарею. Мы знаем, что работа, производимая обратимой электрической батареей, например аккумулятором, равна EΔZ. (Поскольку мы не включили в рассмотрение член PΔV, то придется потребовать, чтобы объем оставался постоянным.) Посмотрим, что скажет о работе батареи термодинамика. Если заменить Р на Е , а V на Z, то вместо уравнения (45.6) получится

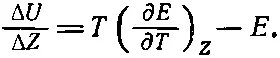(45.9)

Это уравнение говорит нам, что при путешествии заряда ΔZ по батарее меняется внутренняя энергия U . Но почему ΔU/ΔZ — это не просто э. д. с. батареи E? Дело в том, что в реальных обстоятельствах движение зарядов внутри батареи вызывает выделение тепла. Внутренняя энергия батареи изменяется, во-первых, за счет работы, производимой батареей во внешней цепи, и, во-вторых, за счет нагревания батареи. Интересно, что вторую часть изменения внутренней энергии опять-таки можно подсчитать, следя, как меняется э. д. с. батареи при изменении температуры. Между прочим, когда заряды текут по батарее, там происходят химические реакции, и уравнение (45.9) указывает на отличный способ измерения необходимой для реакции энергии. Для этого нам нужно лишь сделать батарею, работающую на этой реакции, и сначала просто измерить э. д. с., а потом проследить, как меняется э. д. с. с температурой, если ни один заряд не выпускается из батареи!

Мы предположили, что объем батареи можно поддерживать постоянным, только поэтому мы позволили себе пренебречь членом PΔV и считать, что работа батареи равна EΔZ. Но оказывается, что поддерживать объем постоянным технически очень трудно. Гораздо легче держать батарею под постоянным атмосферным давлением. Вот почему химики не любят только что написанных нами уравнений: они предпочитают уравнения, которые были бы связаны с постоянным давлением . Мы с самого начала этой главы за независимые переменные приняли V и Т . Химикам больше нравятся Р и Т , поэтому посмотрим теперь, как преобразуются наши выводы при переходе к химической системе переменных. Постарайтесь при этом не ошибиться, потому что мы как-никак сменили детали и перешли от Т и V к Т и Р .

Начнем с (45.3), где ΔU=ΔQ-PΔV; член PΔV можно заменить на E Δ Z или даже на А Δ В . Если бы нам удалось как-нибудь заменить PΔV на VΔP, тогда V и Р поменялись бы ролями и химики остались бы довольны. Тот, кто сообразителен, заметит, что дифференциал произведения PV равен d ( PV )= PdV + VdP . Добавив это равенство к (45.3), он получит

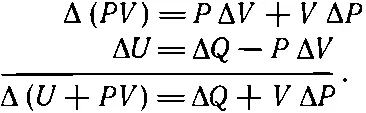
Чтобы все наши последующие выводы походили на выводы из уравнения (45.3), давайте будем считать U+PV какой-то новой функцией, назовем ее энтальпией Н , и напишем в таком виде: ΔH=ΔQ+VΔP.

Вот теперь мы готовы перевести все наши рассуждения на химический язык, надо только помнить, что U → H , Р→-V, V → P . Химики считают, что вся термодинамика содержится не в уравнении (45.7), а в уравнении

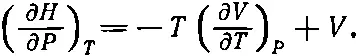
Выяснив, как происходит переход к химическим переменным Т и Р, вернемся к нашим старым переменным. Теперь и уже до конца главы нашими независимыми переменными будут Т и V.

Сейчас давайте применим полученные результаты к некоторым физическим процессам. Сначала рассмотрим идеальный газ. Из кинетической теории известно, что внутренняя энергия газа зависит только от характера движения молекул и от их числа. Внутренняя энергия зависит только от Т , а к V она безразлична. Если изменять V при постоянной Т , то U не изменится. Значит, (∂ U /∂ V ) T =0, и уравнение (45.7) говорит нам, что для идеального газа

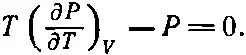(45.10)

Уравнение (45.10) — это дифференциальное уравнение, и оно кое-что расскажет нам о Р . Мы расправимся с частной производной так: поскольку частная производная вычислена при постоянном V , можно заменить частную производную обычной, только надо помнить, что все это делается «при постоянном V ». Уравнение (45.10) тогда принимает вид

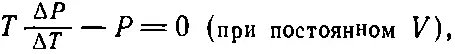(45.11)

интегрирование не составит для нас труда, и мы получим

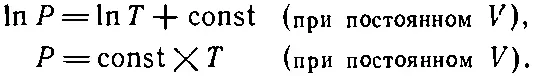(45.12)

Мы знаем, что давление идеального газа равно

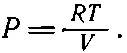(45.13)

Это соотношение совместимо с (45.12), потому что R и V — постоянные. Но зачем же мы мучились, решая эти уравнения? Ведь результат-то был уже известен. Потому что мы пользовались двумя независимыми определениями температуры ! Однажды мы предположили, что кинетическая энергия молекул пропорциональна температуре. Это предположение привело нас к температурной шкале, которую мы назвали шкалой идеального газа. Температура Т в уравнении (45.13) отсчитывается по газовой шкале. Мы называли отсчитанную по газовой шкале температуру кинетической температурой. Потом мы определили температуру иначе, и это определение вообще не нуждалось ни в каком веществе. Исходя из второго закона, мы определили то, что можно назвать «абсолютной термодинамической температурой» Т ; она появляется в уравнении (45.12). Здесь мы только доказали, что давление идеального газа (идеальный газ для нас нечто, чья внутренняя энергия не зависит от объема) пропорционально абсолютной термодинамической температуре. Мы, кроме того, знаем, что давление пропорционально температуре, измеренной по газовой шкале. Таким образом, можно заключить, что кинетическая температура пропорциональна «абсолютной термодинамической температуре». Это, конечно, означает, что если бы мы были благоразумны, то показания обеих шкал могли бы всегда жить в согласии. В конце концов эти шкалы можно выбрать так, что они совпадут; постоянную пропорциональности можно положить равной единице. Очень долго люди сами себе создавали трудности, но наконец превратили две шкалы в одну!