Ричард Фейнман - Том 1. Механика, излучение и теплота

Для члена с а 2мы получаем cos9ωt и cos5ωt, каждый из которых при усреднении превратится в нуль. Для члена с а 9получится cos16ωt и cos(-2ω t ). Но cos(-2ωt) — это то же самое, что cos2ωt, так что опять оба члена дадут при усреднении нуль. Ясно, что все слагаемые с косинусами, за исключением одного, дадут при усреднении нуль. Этим единственным слагаемым будет член с а 7. Для него же мы получим

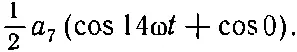(50.7)

Косинус нуля равен единице, а среднее от него, разумеется, тоже равно единице. Итак, мы получили, что среднее от всех членов с косинусами уравнения (50.4) равно 1/ 2а 7.

Еще легче расправиться с синусами. Когда мы умножаем их накосинус типа cos n ω t , то таким же методом можно показать, что все они при усреднении обращаются в нуль.

Мы видим, что способ, придуманный Фурье, действует как своеобразное сито. Когда мы умножаем на cos7ωt и усредняем, то все члены, кроме а 7, отсеиваются и в результате остается

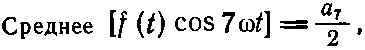(50.8)

или

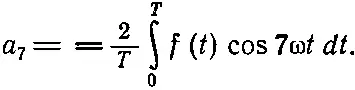(50.9)

Пусть читатель сам докажет, что коэффициенты b 7, например, находятся с помощью умножения (50.2) на sin 7ω t и усреднения обеих частей. Результат таков:

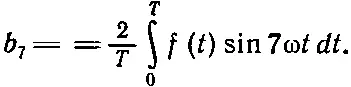(50.10)

Но то, что верно для 7, очевидно, верно и для любого другого целого числа. Теперь мы запишем результат нашего доказательства в следующей, более элегантной математической форме. Если m и n — целые отличные от нуля числа и если ω=2π/T, то

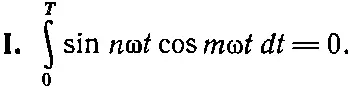(50.11)

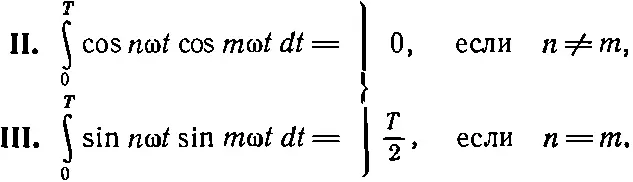(50.12)

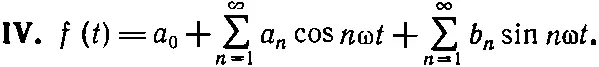(50.13)

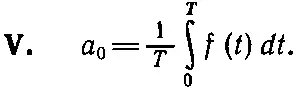(50.14)

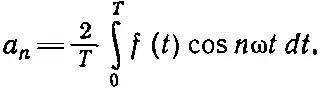(50.15)

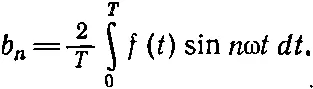(50.16)

В предыдущих главах для описания простого гармонического движения было удобно пользоваться экспоненциальной функцией. Вместо cosωt мы использовали Re ехр(iωt) —действительную часть экспоненциальной функции. В этой главе мы использовали синус и косинус, потому что с ними, пожалуй, немного проще проводить доказательства. Однако наш окончательный результат, уравнение (50.13), можно записать в более компактной форме:

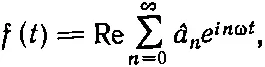(50.17)

где а n — комплексное число а n - ib n (с b 0=0). Если мы всюду будем пользоваться одним и тем же обозначением, то должны также написать

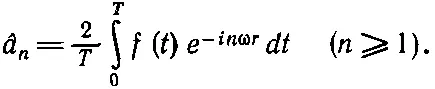(50.18)

Итак, теперь мы умеем раскладывать периодическую волну на ее гармонические компоненты. Эта процедура называется разложением в ряд Фурье , а отдельные члены называются фурье - компонентами . Однако до сих пор мы не показали , что, определив все фурье-компоненты и затем сложив их, мы действительно придем назад к нашей функции f ( t ). Математики доказали, что для широкого класса функций (в сущности, для всех функций, интересных физикам), которые можно проинтегрировать, мы снова получаем f(t). Но есть одно небольшое исключение. Если функция f ( t ) разрывна, т. е. если она неожиданно прыгает от одного значения к другому, сумма Фурье такой функции даст в точке разрыва значение, лежащее посредине между верхним и нижним значениями. Таким образом, если у нас есть странная функция f ( t )=0 для 0≤ t < t 0и f ( t )=1 для t 0≤ t ≤ T , то ее сумма Фурье всюду даст нам правильную величину, за исключением точки t 0, где вместо единицы получится 1/ 2. Во всяком случае, физически даже нельзя требовать, чтобы функция была всюду нулем вплоть до точки t 0, а в самой точке t 0вдруг стала равной единице. Может быть, стоило бы специально для физиков издать такой «указ», что любая разрывная функция (которая может быть только упрощением настоящей физической функции) в точке разрыва должна принимать среднее значение. Тогда любая такая функция, с любым конечным числом «ступенек», как и все другие интересные для физики функции, будет правильно описываться рядом Фурье.

В качестве упражнения предлагаем читателю найти ряд Фурье для функции, показанной на фиг. 50.3.

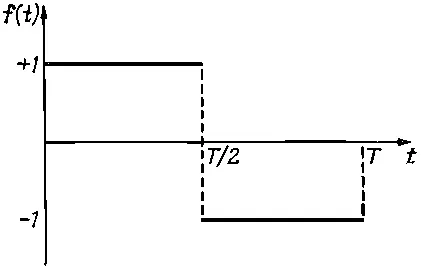
Фиг. 50.3. Ступенчатая функция. f(t)=+1 для 0

Поскольку эту функцию нельзя записать в точной алгебраической форме, то брать интеграл от 0 до Т обычным способом невозможно. Однако если разделить его на две части: по интервалу от 0 до T/2 [на котором функция f(t)=1] и по интервалу от T/2 до T [на котором f ( t ) -1], то интеграл легко берется. В результате должно получиться

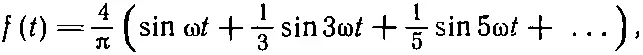(50.19)

где ω=2π/T. Таким образом, оказывается, что для нашей ступенчатой волны (со специально выбранной фазой) будут только нечетные гармоники, причем их амплитуды обратно пропорциональны частотам.

Давайте проверим, что для некоторого значения t результат (50.19) действительно дает снова f ( t ). Возьмем f=T/4или ωt=π/2. Тогда

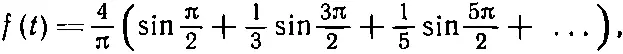(50.20)

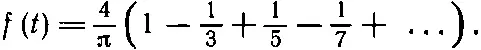(50.21)

Сумма этого ряда [39]равна π/4, а, стало быть, f ( t )=1.

Энергия волны пропорциональна квадрату ее амплитуды. Для сложной волны энергия за один период пропорциональна 0∫ T f 2( t ) dt . Эту энергию можно связать с коэффициентами Фурье. Напишем

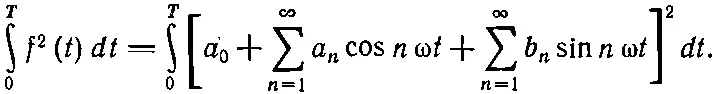(50.22)