Ричард Фейнман - Том 1. Механика, излучение и теплота

В квантовой механике, кроме того, возникают некоторые симметрии, которые, к несчастью, не имеют классического аналога; их нельзя описать методами классической физики. Вот одна из них. Если ψ — это амплитуда некоторого процесса или чего-то другого, то, как мы знаем, квадрат ее абсолютной величины будет вероятностью этого процесса. Пусть теперь некто сделал свои вычисления, используя не ψ, а ψ', которая отличается от ψ только по фазе [т. е. прежняя ψ умножается на ехр(iΔ), где Δ — какая-то постоянная], тогда квадрат абсолютной величины ψ', который тоже будет вероятностью события, равен квадрату абсолютной величины ψ:

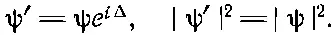(52.1)

Следовательно, физические законы не изменяются от того, что мы сдвигаем фазу волновой функции на некоторую произвольную постоянную. Это еще одна симметрия. Природа физических законов такова, что сдвиг квантовомеханической фазы не изменяет их. В начале этого параграфа мы говорили, что в квантовой механике каждой симметрии соответствует закон сохранения. И вот оказывается, что закон сохранения, связанный с квантовомеханической фазой, не что иное, как закон сохранения электрического заряда . Словом, это удивительнейшая вещь!

Перейдем к следующему вопросу, который будет занимать нас до конца главы,— это симметрия при отражении в пространстве . Проблема заключается в следующем: симметричны ли физические законы при отражении? Можно ее сформулировать и по-другому. Предположим, что мы построили некое устройство, например часы с множеством колесиков, стрелок и пр. Они идут, внутри у них есть устройство для заводки. Посмотрим теперь на часы в зеркало. Дело не в том, как они выглядят в зеркале. Нет, давайте построим другие часы, в точности такие же, как те первые, отраженные в зеркале. Там, где у первых часов находится винт с правой резьбой, мы поставим винт с левой резьбой, там, где на циферблате стоит цифра «XII», мы на циферблате вторых часов нарисуем «IIX», каждая спиральная пружина закручена в одну сторону у первых часов и в противоположную у зеркально отраженных. Когда все будет закончено, получатся двое часов, каждые из которых будут точным зеркальным отражением других, хотя заметьте, что и те и другие настоящие физические материальные объекты. Возникает вопрос: а что, если и те и другие часы запущены при одинаковых условиях, если пружины их закручены одинаково туго, будут ли они идти и тикать, как точное зеркальное отражение? (Это чисто физический, а вовсе не философский вопрос.) Наша интуиция и наше знание физических законов подсказывают, что будут .

Мы подозреваем, что по крайней мере в этом случае отражение будет одной из симметрии физических законов, т. е. если заменить «право» на «лево», а все остальное оставить тем же самым, то никакой разницы при этом мы обнаружить не сможем. Предположим на минуту, что все это верно. Тогда никакими физическими явлениями невозможно различить, где «право», а где «лево», точно так же, как, скажем, никаким физическим опытом невозможно найти абсолютной скорости движения. Таким образом, с помощью каких-то опытов невозможно абсолютно определить, что мы понимаем под «правым», как противоположностью «левого», поскольку все физические законы должны быть симметричны.

Разумеется, мир наш не должен быть симметричным. Если, например, взять то, что мы называем «географией», то здесь вполне можно определить, где правая сторона. Пусть мы находимся в Нью-Орлеане и смотрим в сторону Чикаго. Тогда Флорида будет от нас справа (конечно, если мы стоим ногами на Земле!). Так что в географии можно определить, где «право» и где «лево». В любой системе реальное положение не должно иметь ту симметрию, о которой идет речь, вопрос в том — симметричны ли законы ? Другими словами, противоречит ли физическим законам наличие подобного Земле шара с «левосторонней поверхностью» и человеком, подобным нам, смотрящим в сторону города, подобного Чикаго, с места, подобного Нью-Орлеану, но со всем остальным, перевернутым наоборот, так что Флорида у него будет уже с другой стороны? Ясно, что такая ситуация не кажется невозможной, физическим законам не противоречит такая замена всего левого на правое.

Еще одно обстоятельство: наше определение «правой» стороны не должно зависеть от истории. Иначе было бы очень просто отличить «левое» от «правого» — пойти в магазин запчастей и наугад взять какой-нибудь болт. Вообще говоря, у нас в руках не обязательно окажется «правый болт», но все же более вероятно, что он будет именно правым, а не левым. Но это вопрос истории, или условностей, или общего положения вещей, а не фундаментальных законов. Ведь кто-то может начать выпускать болты с левой резьбой.

Таким образом, нам нужно поискать какие-то другие явления, где бы «правое» входило более фундаментальным образом. Рассмотрим следующую возможность. Известно, что поляризованный свет, пропущенный через сахарный раствор, поворачивает свою плоскость поляризации. Как мы видели в гл. 33 (вып. 3), плоскость поляризации при определенной концентрации сахара поворачивается направо. Казалось бы, мы нашли способ определения «правой стороны», потому что, растворив в воде некоторое количество сахара, мы можем повернуть плоскость поляризации вправо. Но сахар получается из живых организмов, а если мы сделаем его искусственно, то обнаружим, что он не поворачивает плоскости поляризации. Если в этот искусственный сахар, который не поворачивает плоскости поляризации, напустить бактерий (они съедают некоторое количество сахара) и затем отфильтровать их, то обнаружится, что, хотя сахар остался (почти половина первоначального количества), и он поворачивает плоскость поляризации, но теперь уже в другую сторону ! Этот факт кажется очень обескураживающим, однако его можно легко объяснить.

Приведем другой пример. Одно из веществ, общее для всех живых существ, основа жизни — это белки (протеин). Белок состоит из цепочек аминокислот. На фиг. 52.1 показана модель аминокислоты, выделенной из белка.

Фиг. 52.1. Модели молекул аланина. Слева — L-аланин; справа — D-аланин.

Эта кислота названа аланином, и на фиг. 52.1 ( слева ) показано расположение атомов в молекуле аланина, выделенного из белка живых существ. Если же мы попытаемся создать аланин из двуокиси углерода, этана и аммиака (что в самом деле можно сделать — это не столь уже сложная молекула), то обнаружим, что получились не только такие молекулы, но и другие, подобные показанной на фиг. 52.1 ( справа ), причем в равных количествах! Первые молекулы, те, которые произошли от живых существ, называются L - аланином . Другие же, одинаковые с ним химически в том смысле, что состоят из тех же атомов с теми же связями между ними, образуют «правосторонние» молекулы, которые в отличие от «левосторонних» молекул L-аланина называются D - аланином . Интересно, что если мы будем приготовлять аланин в лаборатории из простых газов, то получится смесь обоих сортов в равных количествах. Жизнь, однако, использует только L-аланин. (Но не без исключения, конечно: то там, то здесь в живых существах встречается и D-аланин, однако эти случаи очень редки. Во все белки входит исключительно L-аланин.) Если мы приготовим оба сорта и будем этой смесью кормить животных, которые любят «есть» его (т. е. усваивают аланин), то окажется, что они не смогут использовать D-аланин, а «съедят» только L-аланин. В результате получится то же, что и с нашим сахаром; после того как бактерии «съедят» тот сахар, который им нравится, остается только «ненастоящий» сорт! (Левосторонний сахар тоже сладкий, а все же не такой, как настоящий, правосторонний!)