Ричард Фейнман - Том 1. Механика, излучение и теплота

Итак, похоже, что явления жизни позволяют отличить «правую» сторону от «левой», поскольку две молекулы химически отличны одна от другой. И все-таки — нет, не могут! Пока мы занимались физическими измерениями, подобными определению энергий или скоростей химических реакций и т. д., эти два сорта вели себя совершенно одинаковым образом, если, разумеется, все остальное тоже было зеркально отражено. Одни молекулы поворачивают свет направо, а другие, проходя то же количество раствора,— налево на точно ту же величину. Таким образом, с точки зрения физики можно использовать любую из этих двух аминокислот. Насколько мы понимаем основу вещей сегодня, уже в уравнение Шредингера заложено, что две молекулы должны вести себя в точности одинаковым образом, хотя там, где у одной правая сторона, у другой — левая. Но в природе тем не менее все устроено только одним способом!

Как полагают, причина этого состоит в следующем. Представьте себе, например, что в один прекрасный момент возникли такие условия, что все белки у каких-то существ содержали только левосторонние аминокислоты. Это привело к тому, что все на свете «перекосилось», «перекосились» все вещества в живых клетках, «перекосились» все ферменты— все стало несимметричным. Когда пищеварительные ферменты пытались сменять химию своей пищи с одного сорта на другой, то один сорт пищи «подходил» им, а другой — нет (совсем как золушкин башмачок, с тем исключением, что мы меряем его на «левую ногу»). Насколько нам известно сейчас, в принципе возможно создать такую лягушку, у которой, например, каждая молекула окажется «перевернутой», т. е. создать точное зеркальное отражение настоящей лягушки, так сказать, «левостороннюю» лягушку. Некоторое время эта «левосторонняя лягушка» чувствовала бы себя вполне нормально, но не смогла бы найти себе пищи: если бы она проглотила муху, то ее ферменты не способны были бы переварить ее. Ведь муха-то настоящая, с правосторонней аминокислотой (разумеется, если мы не разведем специально для нашей лягушки «левосторонних мух»). Итак, насколько нам сегодня известно, химические и жизненные процессы, если бы мы все «перевернули», протекали бы точно так же, как и сейчас.

Если жизнь — полностью физико-химическое явление, то факт «закрученности» всех белков только в одном направлении можно понять лишь с той точки зрения, что с самого начала совершенно случайно победил какой-то один сорт молекул. Где-то однажды органическая молекула как-то «перекосилась», и правая сторона оказалась выделенной; какой-то случай в истории создал одностороннюю ситуацию, и с тех пор «перекос» разрастался все шире и шире. Но, возникнув однажды, ситуация, которую мы наблюдаем сейчас, будет продолжаться вечно: все ферменты переваривают и приготовляют только «правосторонние» вещества. Когда в листья растений входит углекислый газ, водяной пар и другие вещества, то ферменты, приготовляющие из них сахар, делают его правосторонним, ибо они сами правосторонние. Если бы в более позднее время возник какой-то новый сорт вирусов или каких-то других живых существ, то они смогли бы выжить только, если оказались бы способны питаться уже существующими органическими веществами. А, стало быть, и сами они должны быть того же сорта.

Для правосторонних молекул не существует закона сохранения их числа. Жизнь может только увеличивать его. Предположение, таким образом, состоит в том, что жизненные явления говорят нам не об отсутствии симметрии физических законов, а, наоборот, об универсальности природы и общности начала всех живых созданий на Земле в описанном выше смысле.

Пойдем дальше. Вы видели, что в физике имеется масса примеров применимости правила правой и левой руки. В самом деле, когда мы изучали векторный анализ, то узнали о правиле правой руки, которым необходимо пользоваться, чтобы получить правильный момент количества движения и момент силы, магнитное поле и т. п. Например, сила, действующая на заряд в магнитном поле, равна F=q v× B. Но представьте себе такое положение: пусть мы знаем F, vи В. Как ив этого узнать, где у нас правая сторона? Если вернуться назад и посмотреть, откуда произошли векторы, то увидим, что правило правой руки — просто соглашение, своего рода трюк. В самом начале такие величины, как угловая скорость и момент количества движения и другие, подобные им, в действительности вообще не были настоящими векторами! Все они каким-то образом связаны с определенными плоскостями, и только благодаря тому, что наше пространство трехмерно, эти величины можно связать с направлением, перпендикулярным данной плоскости. Мы же из двух возможных направлений выбрали правое.

Представьте себе, что какой-то озорной чертик, решив подшутить над физиками, пробрался во все лаборатории и всюду заменил слово «правое» на «левое». И в результате, где было написано правило правой руки, мы вынуждены были бы пользоваться правилом левой руки. Ну что ж, физики бы просто не заметили этого, ибо ни к какому изменению в физических законах это бы не привело, разумеется, если физические законы симметричны.

Покажем это на примере. Вы знаете, что существуют два сорта векторов. Имеются обыкновенные, «настоящие» векторы, подобные, например, отрезку расстояния Δr в пространстве. Пусть в нашей аппаратуре что-то находится «здесь», а нечто другое — «там», тогда те же самые «что-то» будут присутствовать и в зеркально отраженной аппаратуре. Если мы в обоих случаях проведем векторы от «сюда» до «туда», то один вектор будет отражением другого (фиг. 52.2), причем направление стрелки вектора точно, как и все пространство, «выворачивается наизнанку».

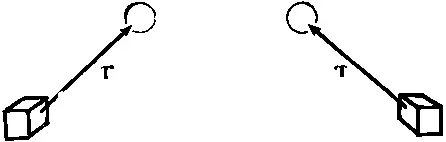
Фиг. 52.2. Отрезок в пространстве и его зеркальное отражение.

Такие векторы мы называем полярными .

Но второй сорт векторов, связанных с вращением, имеет совсем другую природу. Представьте себе нечто вращающееся в трехмерном пространстве (фиг. 52.3).

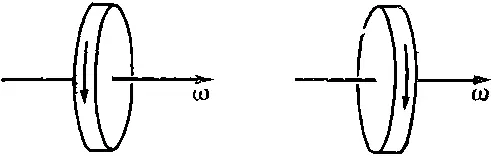
Фиг. 52.3. Вращающееся колесо и его зеркальное отражение. Заметьте, что направление «вектора» угловой скорости не изменяется.

Если посмотреть на это в зеркало, то вращение будет происходить так, как показано на рисунке, т. е. как зеркальное изображение первоначального вращения. Условимся теперь представлять зеркальное вращение с помощью того же самого правила. В результате мы получим «вектор», который в отличие от полярного вектора не изменяется при отражении и оказывается перевернутым по отношению к полярному вектору и геометрии всего пространства. Такой вектор мы называем аксиальным .