Ричард Фейнман - Том 1. Механика, излучение и теплота

Таким образом, F x /| F |=- x / r , или F x =-| F | x / r =- GMmx / r 3и соответственно F y =- GMmy / r 3. Теперь можно воспользоваться динамическими законами (9.7) и написать, что x - или y -компонента ускорения, умноженная на массу планеты, равна соответственно x - или y -компоненте силы:

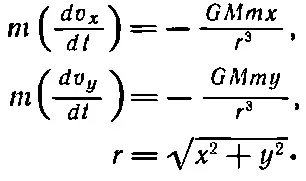(9.17)

Это именно та система уравнений, которую мы должны решить. Для того чтобы упростить вычисления, предположим, что либо единицы измерения времени или массы выбраны соответствующим образом, либо нам просто повезло, словом, получилось так, что GM ≡1. Для нашего случая предположим, что в начальный момент t =0 планета находилась в точке с координатами x =0,500 и y =0,000, а скорость ее в этот момент направлена параллельно оси y и равна 1,6300. Как же в этом случае делаются расчеты? Снова составляется таблица со столбцами для времени t , координаты x, x -компонент скорости v x и ускорения a x . Затем идут отделенные чертой три колонки: для координаты y, y -компонент скорости и ускорения. Однако, для того чтобы подсчитать ускорения, мы должны воспользоваться уравнением (9.17), согласно которому его компоненты равны — x / r 3и — y / r 3, а r =√( x 2+ y 2). Так что, получив x и y , мы должны где-то в сторонке провести небольшие вычисления — извлечь квадратный корень из суммы квадратов и получить расстояние. Удобно также отдельно вычислить и 1/ r 3.

После этого все готово, чтобы определить компоненты ускорения. Всю эту работу можно сильно облегчить, если пользоваться таблицами квадратов, кубов и обратных величин. На нашу долю останется тогда только умножение x на 1/ r 3, которое легко выполняется на логарифмической линейке.

Перейдем к дальнейшему. Возьмем интервал времени ε=0,100. В начальный момент t =0

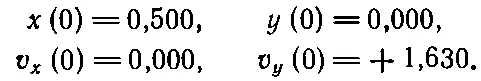
Отсюда находим

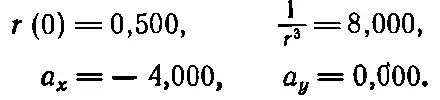
После этого можно вычислять компоненты v x (0,05) и v y (0,05):

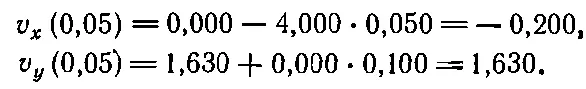
А теперь начнем наш основной расчет:

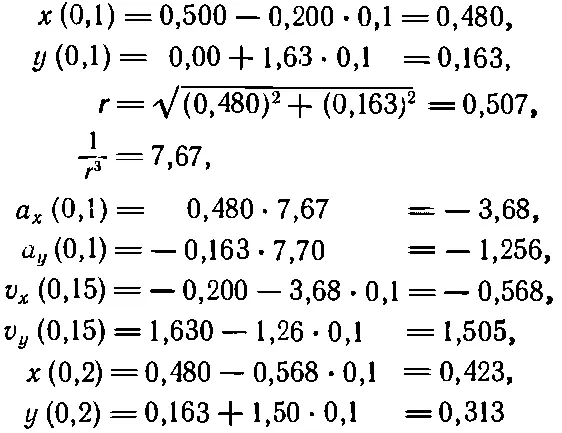
и т. д.

В результате мы получим числа, приведенные в табл. 9.2, где приблизительно за 20 шагов прослежена половина пути нашей планеты вокруг Солнца.

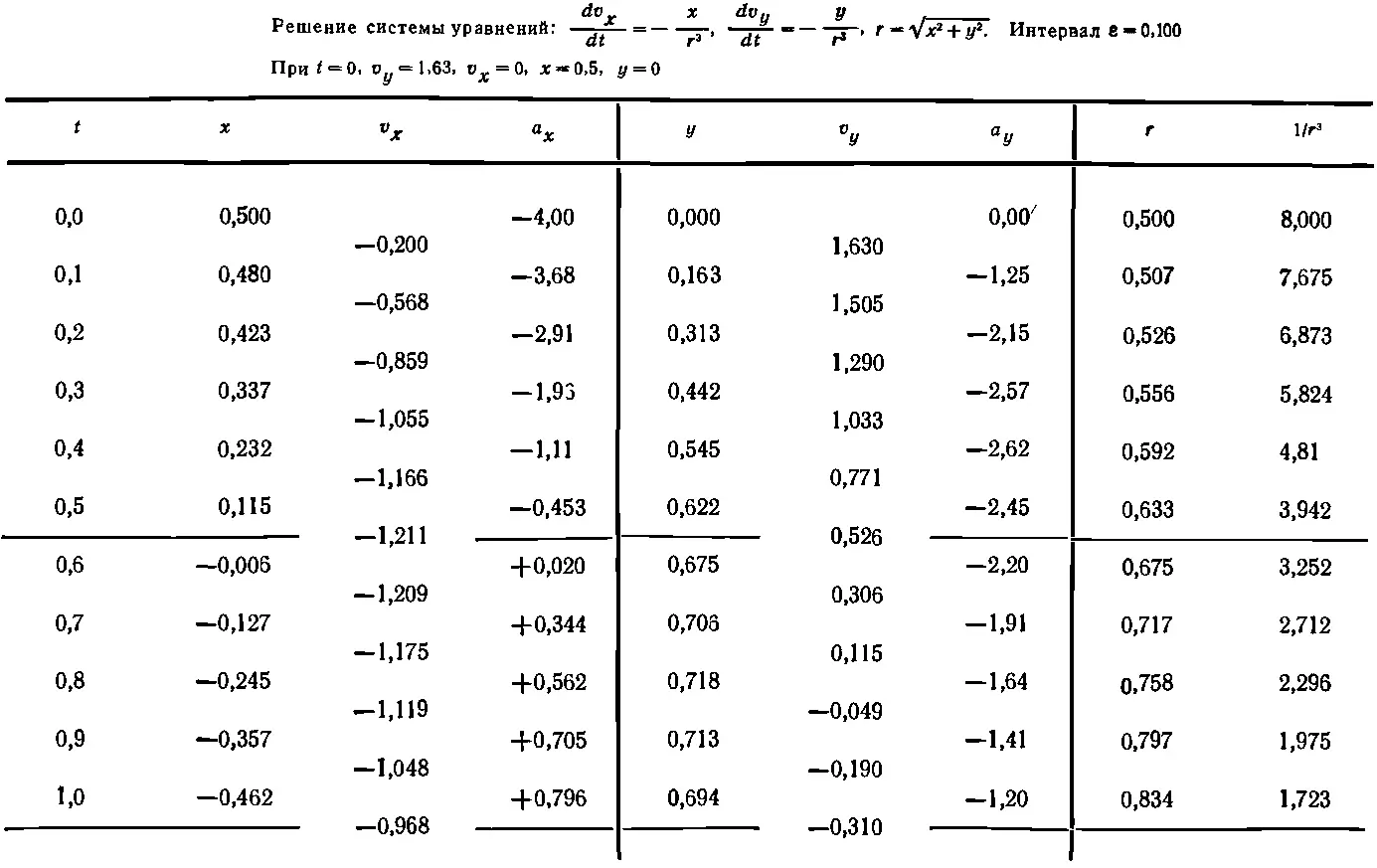
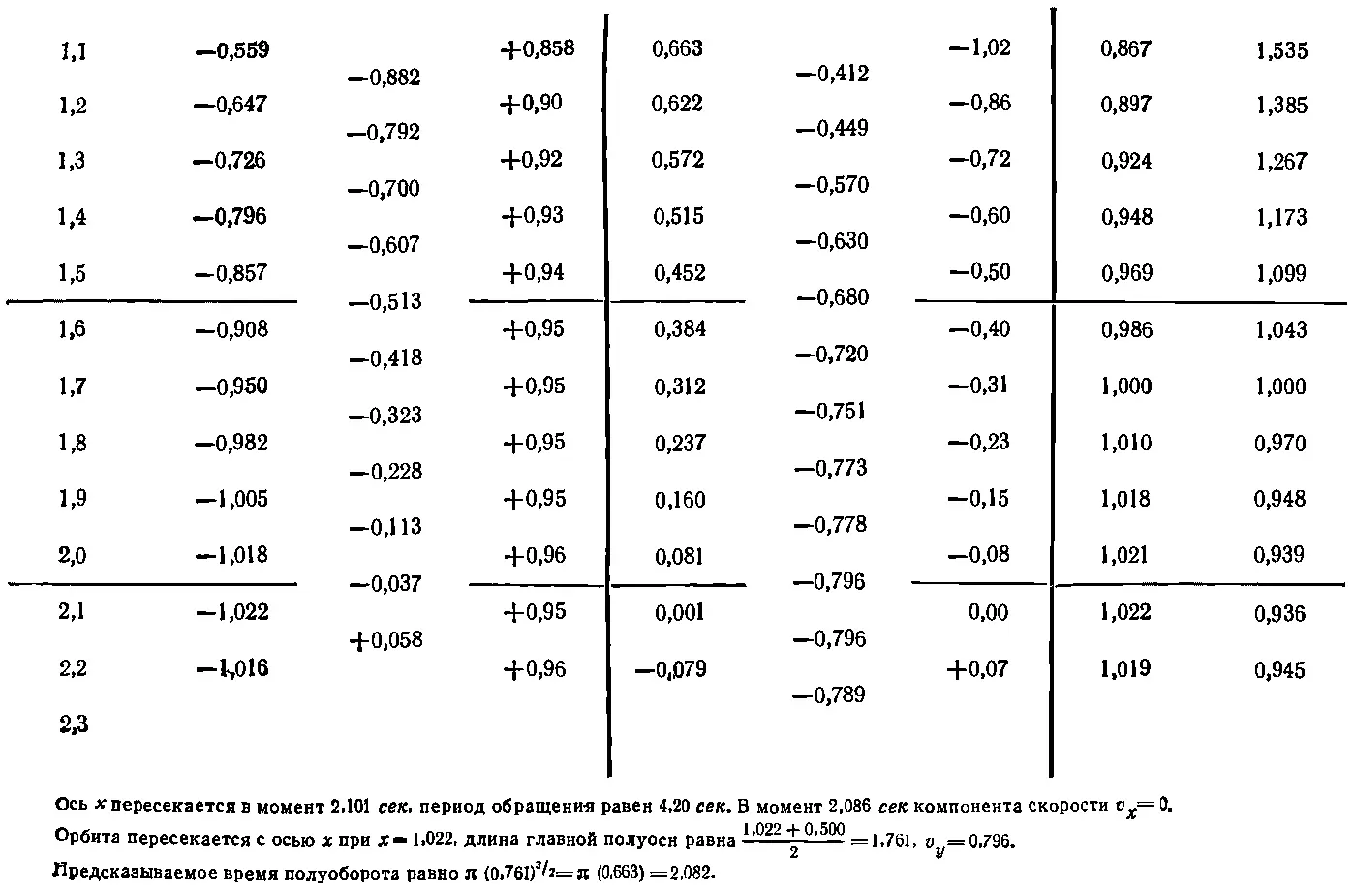
На фиг. 9.6 отложены координаты планеты x и y , приведенные в табл. 9.2.

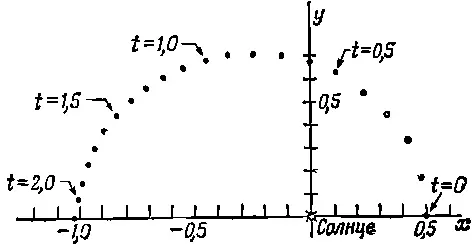
Фиг. 9.6. График движения планеты вокруг Солнца.

Точки представляют собой последовательные положения планеты через каждую десятую долю выбранной нами единицы времени. Видно, что сначала она двигалась быстро, а затем — все медленней и медленней. Видна также и форма кривой движения планеты. Итак, вы теперь знаете, как реально можно вычислять движение планет!

Давайте посмотрим теперь, как вычислить движение Нептуна, Юпитера, Урана и остальных планет. Можно ли сделать подробные расчеты со множеством планет, учитывая к тому же и движение Солнца? Разумеется, можно. Найдем сначала силу, действующую на каждую данную планету, например на ту, которую мы обозначим номером i и координаты которой x i , y i и z i ( i =1 может означать Солнце, i =2 — Меркурий, i =3 — Венеру и т. д.). Наша задача — найти координаты всех планет. По закону тяготения x -компонента силы, действующая на i -ю планету со стороны планеты номер j с координатами x j y j , z j , будет равна — Gm i m j ( x i - x j )/ r ij 3. Если же учесть силы со стороны всех планет, то получим следующую систему уравнений:

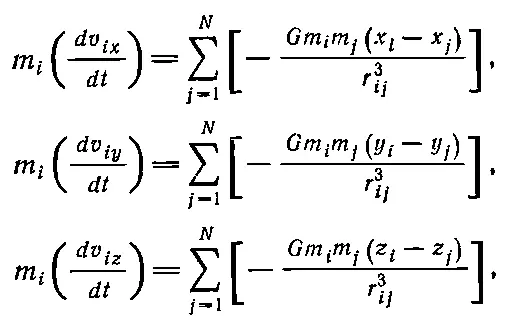(9.18)

где r ij — расстояние между i -й и j -й планетами:

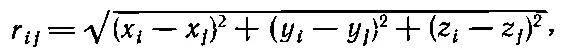(9.19)

а ∑ означает суммирование по всем остальным планетам, r . е. по всем значениям j , за исключением, конечно, j = i . Таким образом, чтобы решить это уравнение, нужно лишь значительно увеличить количество столбцов в нашей таблице. Для движения Юпитера понадобится девять столбцов, для Сатурна — тоже девять и т. д. Если нам заданы все начальные положения и скорости, то из уравнения (9.18) можно подсчитать все ускорения, вычислив, конечно, предварительно по формуле (9.19) все расстояния r ij ,. А сколько же времени потребуется на все эти вычисления? Если вы будете делать их сами дома, то очень много! Однако сейчас уже имеются машины, неимоверно быстро выполняющие все арифметические расчеты. Сложение, например, такая машина выполняет за 1 мксек , т. е. за одну миллионную долю секунды, а умножение — за 10 мксек . Так что если один цикл расчетов состоит из 30 операций умножения, то это займет всего лишь 300 мксек , или за 1 сек можно сделать 3000 циклов. Если мы хотим считать с точностью до одной миллиардной, то для того, чтобы покрыть все время обращения планеты вокруг Солнца, требуется 4·10 5циклов. (Оказывается, что ошибка в расчетах приблизительно пропорциональна квадрату ε. Если брать интервал в тысячу раз меньший, то ошибка уменьшится в миллион раз. Так что для обеспечения нашей точности нужно взять интервал в 10 000 раз меньше.) На машине это займет 130 сек , или около 2 мин . Всего лишь 2 мин , для того чтобы «прогнать» Юпитер вокруг Солнца и при этом еще с точностью до одной миллиардной учесть все возмущения от других планет!

Итак, в начале этой главы для вас были загадкой движения грузика на пружинке, однако теперь вооруженные таким мощным орудием, как законы Ньютона, вы можете вычислять не только такие простые явления, как качание грузика, но и неимоверно сложные движения планет, причем с любой желаемой точностью! Нужна только машина, знающая арифметику.