Ричард Фейнман - Том 1. Механика, излучение и теплота

Несколько слов о силе. В качестве первого грубого приближения мы рассматривали силу как некий толчок или тягу, которая может быть произведена с помощью наших мышц, но теперь, пользуясь уравнением движения, мы можем определить ее более точно. Очень важно помнить, что закон Ньютона включает не только изменение величины импульса, но и изменение его направления. Итак, если масса постоянна, то уравнение (9.1) можно записать в виде

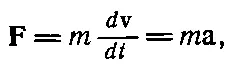(9.2)

где а— ускорение, т. е. «скорость изменения скорости». Второй закон Ньютона означает не только то, что изменения, вызванные данной силой, обратно пропорциональны массе, но и то, что направление изменения скорости совпадает с направлением действия силы. Важно понимать, что термин «ускорение» имеет в физике более широкий смысл, чем в обычной разговорной речи. Он означает не только увеличение скорости, но и замедление ( в этом случае мы говорим, что ускорение отрицательно), и перемену направления движения. В гл. 7 мы уже познакомились с ускорением, направленным под прямым углом к скорости, и мы видели, что предмет, движущийся по окружности радиусом R со скоростью v , за малый интервал времени t уклоняется от своего прямого пути на расстояние 1/ 2( v 2/ R ) t 2. Так что в этом случае ускорение направлено под прямым углом к направлению движения и равно

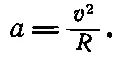(9.3)

Таким образом, сила, действующая под прямым углом к скорости, вызывает искривление пути, причем радиус кривизны можно найти, деля силу на массу тела (при этом мы получаем ускорение) и используя затем формулу (9.3).

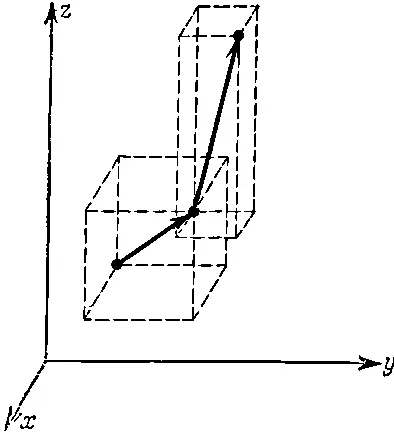
Термин «скорость» тоже имеет в физике более широкий смысл, чем в обыденной жизни. Это не просто некоторое количество метров в секунду, т. е. абсолютная величина скорости, но и направление перемещения в каждый момент времени. Математически мы можем описать и величину, и направление скорости, если будем задавать изменение координат тела с течением времени. Пусть, например, в некоторый момент тело движется так, как это показано на фиг. 9.1.

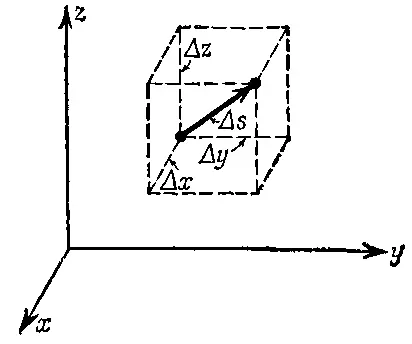
Фиг. 9.1. Малое перемещение тела.

Тогда за малый промежуток времени Δ t оно пройдет некоторое расстояние Δ x в направлении оси x , Δ y в направлении оси y и Δ z в направлении оси z . Результатом же этих изменений координат будет перемещение Δ s вдоль диагонали параллелепипеда со сторонами Δ x , Δ y , Δ z , которые следующим образом связаны с составляющими скорости и интервалом:

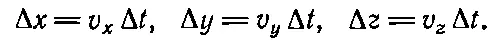(9.4)

В уравнении (9.4) мы разложили скорость на составляющие (или компоненты), которые говорят нам, насколько быстро продвигается тело в направлениях x, y и z . Скорость будет полностью определена как в отношении ее направления, так и абсолютной величины, если задать числовые значения трех ее компонент:

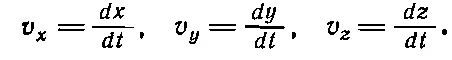(9.5)

При этом абсолютная величина равна

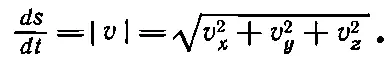(9.6)

Теперь пусть под действием силы меняется не только величина, но и направление скорости (фиг. 9.2).

Фиг. 9.2. Скорость изменяется как по величине, так и по направлению.

Хотя это довольно сложный случай, но с помощью подсчета изменения компонент его рассмотрение сильно упрощается. Изменение x -компоненты скорости за интервал Δ t будет Δ v x = a x Δ t , где а хто, что называется x -компонентой ускорения. Совершенно аналогично Δ v x = a y Δ t и Δ v z=a zΔ t . В такой формулировке Второй закон Ньютона фактически превращается в три закона. Действительно, мы говорим, что сила имеет то же направление, что и ускорение, так что каждая из составляющих силы в направлениях x, y и z равна массе, умноженной на изменение соответствующей компоненты скорости:

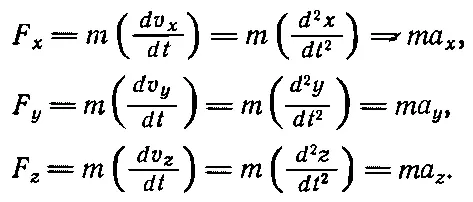(9.7)

Подобно скорости и ускорению, сила тоже может быть разложена на компоненты, причем каждая из них является проекцией отрезка прямой, численно равного абсолютной величине силы и указывающего направление ее действия, на оси x, y и z :

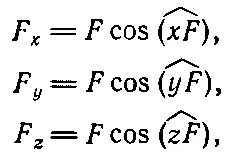(9.8)

где F — абсолютная величина силы, а ( xF ), ( yF ) и ( zF ) — углы между направлением силы и осями x, y и z соответственно.

Уравнения (9.7) представляют собой полную форму Второго закона Ньютона. Зная силы, действующие на тело, и разлагая их на компоненты, можно с помощью этих уравнений найти движение тела. Давайте рассмотрим простой пример. Пусть в направлениях х и у не действуют никакие силы, а есть сила только в направлении z (скажем, вертикально). Тогда, согласно уравнению (9.7), изменяется только одна вертикальная составляющая скорости; что же касается горизонтальных, то они будут оставаться неизменными. Пример такого движения уже рассматривался в гл. 7 (см. фиг. 7.3). Таким образом, горизонтальное движение падающего тела остается неизменным, тогда как в вертикальном направлении оно движется так, как будто никакого горизонтального движения вообще нет. Другими словами, если компоненты сил не связаны друг с другом, то и движения в направлениях осей x, y и z будут независимы.

Чтобы пользоваться законами Ньютона, мы должны иметь какую-то формулу для сил; ведь эти законы говорят нам: подумайте о силах. Если тело ускоряется, стало быть, на него что-то действует. А как найти это «что-то»? Нашей программой на будущее должно быть отыскание законов для сил. Некоторые из таких законов были найдены самим Ньютоном. Например, формула для силы тяготения. Часть сведений о силах другого рода содержится в Третьем законе, который утверждает равенство сил действия и противодействия, но об этом более подробно пойдет речь в следующей главе.