Ричард Фейнман - Том 1. Механика, излучение и теплота

Предположим теперь, что существует другая направленная величина, например сила — еще одна величина, которую можно определить, задав связанные с ней три числа. Эти три числа переходят при изменении системы координат в другие три числа по строго определенным математическим правилам. Эти правила должны быть теми же самыми, которые определяли переход тройки чисел x, y, z в х ' , у ', z '. Другими словами, вектор — это величина, определяемая тремя числами, которые преобразуются при изменениях системы координат так же, как составляющие шага в пространстве. Уравнение типа

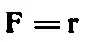
справедливо в любой системе координат, если оно верно хотя бы в одной из них. Оно заменяет нам три уравнения

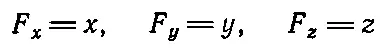
или соответственно

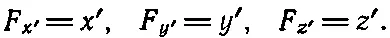
Тот факт, что физические соотношения между какими-либо величинами можно выразить в виде векторных уравнений, говорит о том, что эти соотношения верны в любой системе координат. Вот почему понятие вектора очень удобно в физике.

Давайте теперь рассмотрим некоторые свойства векторов. В качестве примера «вектора» можно указать скорость, импульс, силу и ускорение. Часто бывает удобно изобразить вектор в виде стрелки, указывающей направление действия. Но почему же можно представить силу стрелкой? Да потому, что она преобразуется по тем же законам, что и «шаг в пространстве». Именно поэтому можно представить силу в виде чертежа, как если бы это изображалось перемещение, причем выберем такой масштаб, чтобы единица силы, например ньютон, соответствовала некоторой длине. Проделав такую процедуру однажды, мы всегда сможем изображать силы в виде отрезков, потому что уравнение типа

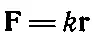
(где k — некоторая постоянная) имеет вполне определенный смысл. Возможность представлять силу отрезком сулит нам большие выгоды, потому что, изобразив отрезок или стрелку, можно не заботиться о координатных осях. При этом, конечно, всегда можно быстро подсчитать, как изменяются составляющие вектора при поворотах осей, потому что дело сводится к простому геометрическому построению.

Теперь мы должны описать законы, или правила, регулирующие возможные сочетания различных векторов. Прежде всего мы изучим сумму двух векторов. Пусть векторы aи bзадаются в какой-нибудь системе координат составляющими а x , a y , a z и b x , b y , b z . Предположим, что кому-то пришло в голову составить три числа а x + b x , a y + b y , а z + b z . Получим ли мы в результате вектор? Вы можете сказать: «Разумеется, ведь это три числа, а три числа образуют вектор». Нет, вектор образуют не любые три числа! Чтобы задать вектор, мы должны связать заданные нам три числа с координатной системой так, чтобы при повороте координатных осей эти числа «поворачивались» относительно друг друга и «перемешивались» по описанным ранее правилам. Таким образом, мы должны выяснить, во что превращаются числа а x + b x , а y + b y , a z + b z , если известно, что при изменении системы координат числа а x , а у , a z переходят в а ' x , а ' у , a ' z , а b x , b у , b z переходят в b ' x , b ' y , b ' z? Получим ли мы после поворота координатных осей числа а ' x + b ' x , a ' y + b ' y , a ' z + b ' z ? Ответ, конечно, будет утвердительным, потому что наше основное уравнение (11 :5) определяет так называемое линейное преобразование. Если мы применим это преобразование к а x и b x и вычислим а x + b x то окажется, что преобразованное а x + b x есть то же самое, что и а x + b x . «Складывая» векторы аи bпо только что описанному правилу, мы получаем новый вектор c. Мы запишем это так:

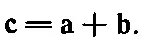
Вектор с обладает интересным свойством:

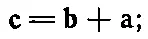
это легко проверить, написав составляющие вектора с. Кроме того,

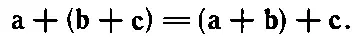
Векторы можно складывать в любом порядке.

Каков геометрический смысл a+ b? Как будет выглядеть вектор с, если мы, скажем, изобразим aи bс помощью стрелок? Ответ на этот вопрос дает фиг. 11.4.

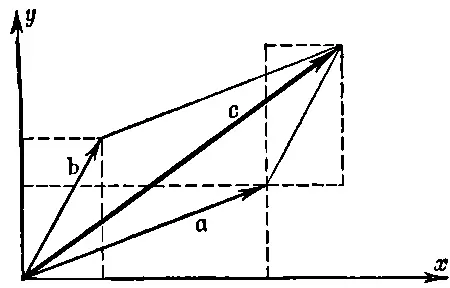
Фиг. 11.4 .Сложение векторов.

Мы видим, что прибавить составляющие вектора bк составляющим вектора апроще всего, приложив соответствующим образом прямоугольник, определяемый составляющими b, к такому же прямоугольнику, определяемому составляющими a. Поскольку aи bхорошо подогнаны к своим прямоугольникам, то это все равно, что поставить вектор b«ногами» на «голову» вектору a. Стрелка, соединяющая «ноги» вектора аи «голову» вектора b, и будет вектором с. Можно поступить иначе: поставить «ноги» aна «голову» b. Вспомнив геометрические свойства параллелограмма, можно убедиться в том, что мы снова получим тот же вектор c. Заметим, что, ставя векторы друг на друга, мы складываем их без помощи координатных осей.

Предположим, что мы умножили вектор aна число α. Что нужно понимать под таким произведением? Договоримся понимать под этим вектор с компонентами α а x , α а у , α a z . Докажите сами, что это действительно вектор.

Рассмотрим теперь вычитание векторов. Можно определить вычитание тем же способом, что и сложение, но вместо того, чтобы складывать, будем вычитать составляющие. Можно также определить вычитание как сложение с отрицательным вектором - b=(-1) b. Результат будет тот же.