Ричард Фейнман - Том 1. Механика, излучение и теплота

Итак, уравнения для энергии и импульса имеют вид

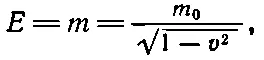
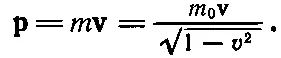(17.6)

Значит, при таком выборе единиц получится

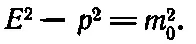(17.7)

Скажем, если энергия выражена в электронвольтах (эв), то чему равна масса в 1 эв? Она равна массе с энергией покоя 1 эв , т. е. m 0c 2=1 эв . У электрона, например, масса покоя равна 0,511·10 6 эв .

Как же будут выглядеть импульс и энергия в новой системе координат? Чтобы узнать это, надо преобразовать уравнения (17.6). Это преобразование легко получить, зная, как преобразуется скорость. Пусть некоторое тело имело скорость v , а мы наблюдаем за ним из космического корабля, который сам имеет скорость u , и обозначаем соответствующие величины штрихами. Для простоты сперва мы рассмотрим случай, когда скорость v направлена по скорости u . (Более общий случай мы рассмотрим позже.) Чему равна скорость тела v ' по измерениям из космического корабля? Эта скорость равна «разности» между v и u . По прежде полученному нами закону

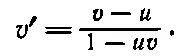(17.8)

Теперь подсчитаем, какой окажется энергия Е ' по измерениям космонавта. Он, конечно, воспользуется той же массой покоя, но зато скорость станет v '. Он возведет v ' в квадрат, вычтет из единицы, извлечет квадратный корень и найдет обратную величину

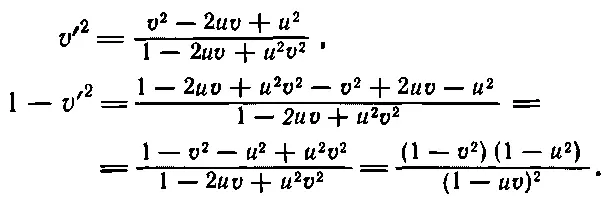
Поэтому

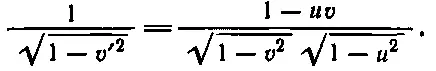(17.9)

Энергия Е ' просто равна массе m 0, умноженной на это выражение. Но нам хочется выразить энергию через нештрихованные энергию и импульс. Мы замечаем, что

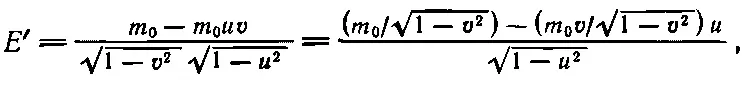
или

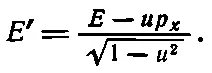(17.10)

Мы узнаем в этом выражении знакомое нам преобразование

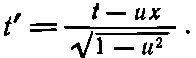
Теперь мы должны найти новый импульс р ' x . Он равен энергии Е ', умноженной на v ', и так же просто выражается через Е и р :

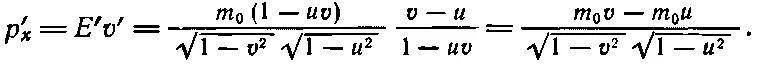
Итак,

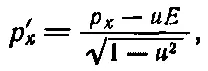(17.11)

и мы опять распознаем в этой формуле знакомое нам

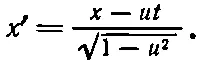
Итак, преобразование старых энергии и импульса в новые энергию и импульс в точности совпало с преобразованием t и х в t ' и х и t в х ': если мы в уравнениях (17.4) будем писать Е каждый раз, когда увидим t , а вместо x: всякий раз будем подставлять р x , то уравнения (17.4) превратятся в уравнения (17.10) и (17.11). Если все верно, то это правило предполагает добавочные равенства р ' у =- р y и р ' z = р z . Чтобы их доказать, надо посмотреть, как преобразуется движение вверх или вниз. Но как раз в предыдущей главе мы рассмотрели такое движение. Мы анализировали сложное столкновение и заметили, что поперечный импульс действительно не меняется при переходе в движущуюся систему координат. Стало быть, мы уже убедились, что р ' у = р у и p z = p z . Итак, полное преобразование равно

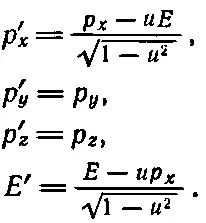(17.12)

Таким образом, эти преобразования выявили четыре величины, которые преобразуются подобно x, y, z, t . Назовем их четырехвектор импульса . Так как импульс — это четырехвектор, его можно изобразить на диаграмме пространства-времени движущейся частицы в виде «стрелки», касательной к пути (фиг. 17.4).

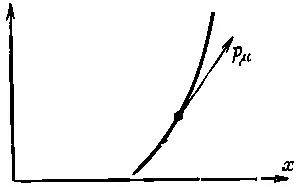
Фиг. 17.4. Четырехвектор импульса частицы.

У этой стрелки временная компонента дает энергию, а пространственные — тривектор импульса; сама стрелка «реальнее», чем один только импульс или одна лишь энергия: ведь и импульс, и энергия зависят от нашей точки зрения.

Четырехвекторы обозначаются иначе, чем тривекторы. Например, тривектор импульса обозначают р. Если хотят дать более детальную запись, то говорят о трех компонентах р x , p у , р z ; можно писать и короче р i , оговаривая, что i принимает три значения x, y и z. Для четырехвекторов мы будем применять похожее обозначение: будем писать р μ, а μ пусть заменяет собой четыре направления t, x, у, z .

Конечно, можно пользоваться любыми обозначениями. Не улыбайтесь, что мы так много говорим об обозначениях; учитесь изобретать их: в них вся сила. Ведь и сама математика в значительной степени состоит в изобретении лучших обозначений. Идея четырехвектора — это тоже усовершенствование обозначений с таким расчетом, чтобы преобразования было легче запомнить.

Итак, A μ— это общий четырехвектор, р μ— четырехимпульс, p t — энергия, р x — импульс в направлении х, р y — в направлении у, p z — в направлении z. Складывая четырехвекторы, складывают их соответствующие компоненты.

Если четырехвекторы связаны каким-то уравнением, то это значит, что уравнение выполняется для любой компоненты . Например, если закон сохранения тривектора импульса соблюдается в столкновении частиц, т. е. сумма импульсов множества взаимодействующих или сталкивающихся частиц постоянна, то это означает, что сумма всех компонент импульсов постоянна и в направлении х , и в направлении у , и в направлении z . Сам по себе такой закон в теории относительности невозможен: он неполон ; это все равно, что говорить только о двух компонентах тривектора. Неполон он потому, что при повороте осей разные компоненты смешиваются, значит, в закон сохранения должны войти все три компоненты. Таким образом, в теории относительности нужно дополнить закон сохранения импульса, включив в него сохранение временной компоненты. Абсолютно необходимо , чтобы сохранение первых трех компонент сопровождалось сохранением четвертой, иначе не получится релятивистской инвариантности. Четвертое уравнение — это как раз сохранение энергии ; оно должно сопровождать сохранение импульса для того, чтобы четырехвекторные соотношения в геометрии пространства-времени были справедливы.