Ричард Фейнман - Том 2. Электромагнетизм и материя

Итак, если нам очень хочется , мы можем выбросить весь набор сил в уравнении (28.9), приговаривая при этом, что такое явление, как действие электрона на себя, отсутствует. Но вместе с водой мы выплескиваем и ребенка! Ведь второе-то слагаемое в (28.9), слагаемое с ... х , совершенно необходимо. Эта сила приводит к вполне определенному эффекту. Если вы ее выбросите — беды не миновать. Когда вы разгоняете заряд, он излучает электромагнитные волны, т. е. теряет энергию. Поэтому ускорение заряда требует большей силы, чем ускорение нейтрального объекта той же массы; в противном случае энергия не будет сохраняться. Скорость, с которой мы затрачиваем работу на ускорение заряда, должна быть равна скорости потери энергии на излучение. Мы уже говорили об этом эффекте; он был назван радиационным сопротивлением. Снова перед нами вопрос: откуда берутся те дополнительные силы, на преодоление которых затрачивается эта работа? Когда излучает большая антенна, то эти силы возникают под влиянием токов одной ее части на токи в другой. Но у отдельного ускоряющегося электрона, излучающего в пустое пространство, возможен только один источник таких сил — действие одной части электрона на другую.

В гл. 32 (вып. 3) мы обнаружили, что осциллирующий заряд излучает энергию со скоростью

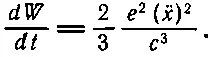(28.10)

Давайте посмотрим, какая мощность необходима для преодоления силы самодействия (28.9). Мощность, как известно, равна силе, умноженной на скорость, т. е. F . x :

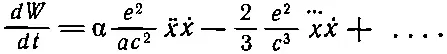(28.11)

Первый член пропорционален d . x 2/ dt и поэтому соответствует скорости изменения кинетической энергии 1/ 2 mv 2, связанной с электромагнитной массой. А второй соответствует излучению мощности (28.10). Однако он отличается от (28.10). Разница состоит в том, что (28.11) справедливо в общем случае, тогда как (28.10) верно только для осциллирующего заряда. Мы можем доказать, что эти два выражения для периодического движения заряда эквивалентны. Перепишем для этого второй член выражения (28.11) в виде

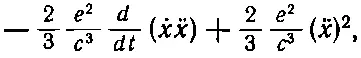
что будет просто алгебраическим преобразованием. Если движение электрона периодическое, то величина хх периодически возвращается к одному и тому же значению. Так что если мы возьмем среднее значение ее производной по времени, то получим нуль. Однако второй член всегда положителен (как квадрат величины), так что его производная тоже положительна. Соответствующая ему мощность как раз равна выражению (28.10).

Итак, слагаемое с ... x в выражении для силы самодействия необходимо для сохранения энергии излучающей системы и не может быть выброшено. Это было одним из триумфов теории Лоренца, доказавшего возникновение такого слагаемого в результате воздействия электрона самого на себя. Мы вынуждены поверить в идею самодействия и необходимость слагаемого с ... х . Проблема в том, как сохранить его, избавившись при этом от первого слагаемого в выражении (28.9), которое портит все дело. Этого мы не знаем. Как видите, классическая теория электрона сама себя завела в тупик.

Были предприняты и другие попытки выправить положение. Один путь был предложен Борном и Инфельдом. Состоит он в очень сложном изменении уравнений Максвелла, так что они перестают быть линейными. При этом можно сделать так, чтобы энергия и импульс оказались конечными. Но предложенные ими законы предсказывают явления, которые никогда не наблюдались. Их теория страдает еще и другим недостатком, к которому мы придем позднее и который присущ всем попыткам избежать описанную трудность.

Следующая интересная возможность была предложена Дираком. Он рассуждал так: давайте допустим, что действие электрона на себя описывается не первым слагаемым выражения (28.9), а вторым . И тогда ему пришла заманчивая идея избавиться от первого слагаемого, сохранив при этом второе. Смотрите — сказал он,— когда мы брали только запаздывающие решения уравнений Максвелла, это условие выступало как дополнительное предположение; если бы вместо запаздывающих мы взяли опережающие волны, то ответ получился бы несколько другим. Выражение для силы самодействия приобрело бы вид

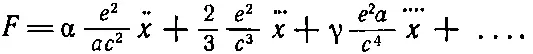(28.12)

Это выражение в точности такое же, как и (28.9), за исключением знака перед вторым и некоторыми высшими членами ряда. [Замена запаздывающих волн опережающими означает просто смену знака запаздывания, что, как нетрудно видеть, эквивалентно изменению знака t . В выражении (28.9) это приводит только к изменению знака всех нечетных производных.] Итак, Дирак предложил: давайте примем новое правило, что электрон действует на себя полуразностью создаваемых им запаздывающих и опережающих полей. Полуразность выражений (28.9) и (28.12) дает

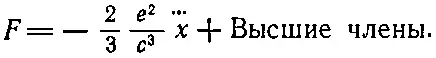
Во всех высших членах радиус а входит в числитель в положительной степени. Поэтому, когда мы переходим к пределу точечного заряда, остается только один член — как раз тот, который нам нужен. Таким путем Дирак сохранил радиационное сопротивление и избавился от силы инерции. Электромагнитная масса исчезла, классическая теория спасена, но благополучие это достигнуто ценой насилия над самодействием электрона.

Произвол дополнительных предположений Дирака был устранен, по крайней мере до некоторой степени, Уилером и Фейнманом, которые предложили еще более странную теорию. Они предположили, что точечный заряд взаимодействует только с другими зарядами, но взаимодействие идет наполовину через запаздывающие, наполовину через опережающие волны. Самое удивительное, как оказалось, что в большинстве случаев вы не видите эффекта опережающих волн, но они дают как раз нужную силу радиационного сопротивления. Однако радиационное сопротивление возникает не как самодействие электрона, а в результате следующего интересного эффекта. Когда электрон ускоряется в момент t, то он влияет на все другие заряды в мире в поздний момент t '= t + r / c (где r — расстояние до других зарядов) из-за запаздывающих волн. Но затем эти другие заряды действуют снова на первоначальный электрон с помощью опережающих волн, которые приходят к нему в момент t", равный t ' минус r / c , что как раз равно t . (Они, конечно, воздействуют и с помощью запаздывающих волн, но это просто соответствует обычным «отраженным» волнам.) Комбинация опережающих и запаздывающих волн означает, что в тот момент, когда электрон ускоряется, осциллирующий заряд испытывает воздействие силы со стороны всех зарядов, которые «приготовились» поглотить излученные им волны. Вот в какой петле запутались физики, пытаясь спасти теорию электрона!