Ричард Фейнман - Том 2. Электромагнетизм и материя
- Название:Том 2. Электромагнетизм и материя
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 2. Электромагнетизм и материя краткое содержание
Том 2. Электромагнетизм и материя - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Чтобы получить полную энергию, нужно эту плотность проинтегрировать по всему пространству. Используя элемент объема 4πr 2dr, найдем полную энергию, которую мы обозначим через U эл :
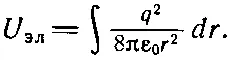
Это выражение интегрируется очень просто. Нижний предел интегрирования равен а, а верхний — бесконечности, поэтому
 (28.1)
(28.1)
Если вместо q подставить заряд электрона q e и обозначить символом e 2комбинацию q e 2/4πε 0, то получим
 (28.2)
(28.2)
Все идет хорошо до тех пор, пока мы не переходим к точечному заряду, т. е. пока мы не положим а=0. Но как только мы переходим к точечному заряду, начинаются все наши беды. И все потому, что энергия поля изменяется обратно пропорционально четвертой степени расстояния, интеграл по объему становится расходящимся, а количество энергии, окружающей точечный заряд, оказывается бесконечным.
Но чем, собственно, плоха бесконечная энергия? Есть ли какая-то реальная трудность в том, что энергия никуда не может уйти от заряда и обречена навсегда оставаться около него? Досадно, конечно, что величина оказалась бесконечной, но главный вопрос в том — есть ли здесь какой-нибудь наблюдаемый физический эффект? Чтобы ответить на него, нужно обратиться не к энергии, а к чему-то другому. Нас может, скажем, заинтересовать, как изменяется энергия, когда заряд движется . Если при этом окажется бесконечным изменение , то дело совсем плохо.
§ 2. Импульс поля движущегося заряда
Возьмем равномерно движущийся электрон и предположим на минуту, что скорость его мала по сравнению со скоростью света. С таким движущимся электроном всегда связан какой-то импульс — даже если у электрона до того, как он был заряжен, не было никакой массы — это импульс электромагнитного поля. Мы покажем, что для малых скоростей он пропорционален скорости v и совпадает с ней по направлению. В точке Р , находящейся на расстоянии r от центра заряда и под углом θ к линии его движения (фиг. 28.1), электрическое поле радиально, а магнитное, как мы видели, равно v×E/c 2.

Фиг. 28.1. Поля Еи Ви плотность импульса gдля положительного электрона. Для отрицательного электрона поля Еи Вповернуты в обратную сторону, но g остается тем же.
Плотность же импульса, в соответствии с формулой (27.21), будет
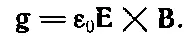
Она обязательно направлена по линии движения, как это видно из рисунка, и по величине равна
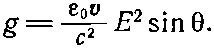
Поле симметрично относительно линии движения заряда, поэтому поперечные компоненты дадут в сумме нуль, и полученный в результате импульс будет параллелен скорости v. Величину составляющей вектора gв этом направлении, равную g sinθ, нужно проинтегрировать по всему пространству. В качестве элемента объема возьмем кольцо, плоскость которого перпендикулярна v(фиг. 28.2).
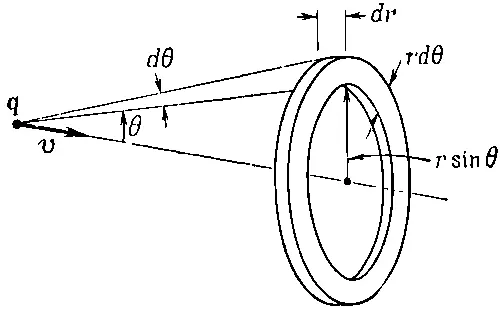
Фиг. 28.2. Элемент объема 2πr 2 sinθdθdr, используемый при вычислении импульса поля.
Объем его равен 2πr 2sinθdθdr. Полный импульс будет при этом

Поскольку Е не зависит от угла θ (для v ≪ c ), то по углу можно немедленно проинтегрировать:

Интегрирование по θ ведется в пределах от 0 до π, так что этот интеграл дает просто множитель 4/ 3, т. е.
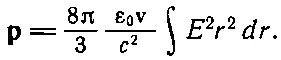
А такой интеграл (для v≪с) мы только что вычисляли, чтобы найти энергию; он равен q 2/16π 2ε 0 2 a , так что

или
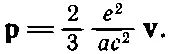 (28.3)
(28.3)
Импульс поля, т. е. электромагнитный импульс, оказался пропорциональным v. В частности, тоже самое выражение получилось бы для частицы с массой, равной коэффициенту пропорциональности при v. Вот почему этот коэффициент пропорциональности мы можем назвать электромагнитной массой m эм , т. е. положить
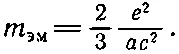
§ 3. Электромагнитная масса
Откуда же вообще возникло понятие массы? В наших законах механики мы предполагали, что любому предмету присуще некое свойство, называемое массой. Оно означает пропорциональность импульса предмета его скорости. Теперь же мы обнаружили, что это свойство вполне понятно — заряженная частица несет импульс, который пропорционален ее скорости. Дело можно представить так, как будто масса — это просто электродинамический эффект. Ведь до сих пор причина возникновения массы оставалась нераскрытой. И вот, наконец, в электродинамике нам представилась прекрасная возможность понять то, чего мы никогда не понимали раньше. Прямо как с неба (а точнее, от Максвелла и Пойнтинга) свалилось на нас объяснение пропорциональности импульса любой заряженной частицы ее скорости через электромагнитные свойства.
Но давайте все-таки встанем на более консервативную точку зрения и будем говорить, по крайней мере временно, что имеется два сорта масс и что полный импульс предмета должен быть суммой механического и электромагнитного импульсов. Причем механический импульс равен произведению «механической» массы m мехна скорость v. В тех экспериментах, где масса частицы измеряется, например, определением импульса или «кручением на веревочке», мы находим ее полную массу. Импульс равен произведению именно полной массы ( m мех + m эм ) на скорость. Таким образом, наблюдаемая масса может состоять из двух (а может быть, и из большего числа, если мы учтем другие поля) частей: механической и электромагнитной. Мы знаем, что наверняка имеется электромагнитная часть; для нее у нас есть даже формула. А сейчас появилась увлекательная возможность выбросить механическую массу совсем и считать массу полностью электромагнитной.
Читать дальшеИнтервал:
Закладка:






