Ричард Фейнман - Том 2. Электромагнетизм и материя

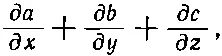
поскольку x -компонента импульса должна течь в каком-либо из трех направлений. Во всяком случае, каковы бы ни были а, b и с, такая комбинация предполагается равной потоку x -компоненты импульса.

Дальше по правилам той же самой игры напишем ρ Е+ j× Bтолько через Еи В, исключив плотность заряда ρ и плотность тока jи затем жонглируя слагаемыми и произведя подстановку, получаем

Сопоставляя затем разные слагаемые, мы должны найти выражения для g x , a, b и с . В общем, здесь масса работы, но мы не собираемся заниматься ею. Вместо этого мы найдем только выражение для плотности импульса gи притом совсем другим способом.

В механике есть очень важная теорема, которая говорит: каков бы ни был поток энергии любого вида (энергия поля или какой-то другой сорт энергии), произведение ее количества, прошедшего через единицу площади в единицу времени, на 1/ с 2равно импульсу в единице объема пространства. В случае электродинамики эта теорема говорит, что gравно вектору Пойнтинга, поделенному на с 2:

(27.21)

Так что вектор Пойнтинга дает нам не только поток энергии, но после деления на с 2и плотность импульса. Этот же результат получился бы из анализа, который мы только что предполагали проделать, однако более заманчиво воспользоваться общей теоремой. Сейчас мы рассмотрим несколько интересных примеров и рассуждений, призванных убедить вас в справедливости этой общей теоремы.

Первый пример: возьмем множество заключенных в ящик частиц. Пусть, скажем, их будет N штук на кубический метр, и пусть они движутся вдоль ящика со скоростью v. Рассмотрим теперь воображаемую плоскость, перпендикулярную к v. Поток энергии через единицу площади этой плоскости в секунду равен Nv (т. е. числу частиц, пересекающих плоскость за секунду), умноженному на энергию каждой частицы. Энергия же каждой частицы будет m 0 c 2/√(1- v 2/ c 2). Так что поток энергии равен

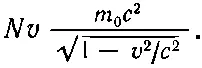
Но импульс каждой частицы равен m 0 v √(1- v 2/ c 2), откуда плотность импульса будет

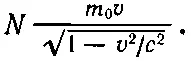
что в полном согласии с теоремой как раз равно 1/ с 2на поток энергии. Таким образом, для пучка частиц теорема оказывается верной.

Верна она и для света. При изучении света (см. вып. 3) мы установили, что, когда происходит поглощение света, поглотителю передается некоторое количество импульса. Действительно, в гл. 34 (вып. 3) мы видели, что импульс равен поглощенной энергии, деленной на с [уравнение (34.24)]. Пусть U 0будет энергией, падающей в секунду на единичную площадь, тогда переданный той же поверхности за то же время импульс равен U 0/ c . Но импульс распространяется со скоростью с , так что его плотность перед поглотителем должна быть равна U 0/ с 2. Теорема снова справедлива.

Наконец, я приведу рассуждение Эйнштейна, которое еще раз продемонстрирует то же самое утверждение. Предположим, у нас есть вагон с какой-то большой массой М , который может без трения катиться по рельсам. В одном его конце расположено устройство, способное «выстреливать» какие-то частицы или световой импульс (совершенно безразлично, чем оно стреляет), которые ударяются о противоположный конец вагона. Следовательно, некоторое количество энергии, скажем U , находившееся первоначально на одном конце (фиг. 27.7,а), перелетает на противоположный конец (фиг. 27.7,в).

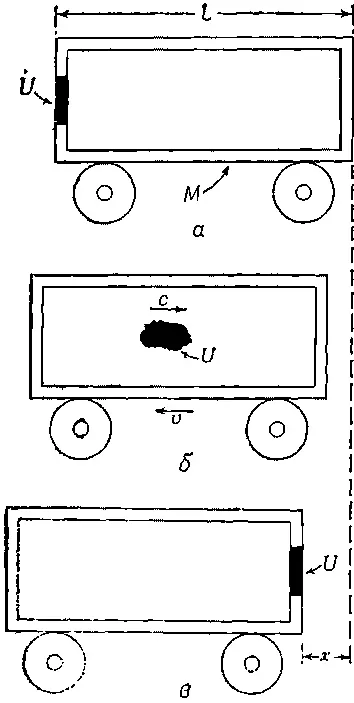
Фиг. 27.7. Порция энергии U, двигаясь со скоростью с, несет импульс, равный U/c.

Таким образом, энергия U перемещается на расстояние, равное длине вагона L . Этой энергии U соответствует масса U/с 2, так что если вагон вначале стоял, то его центр масс должен передвинуться. Эйнштейну не понравилось заключение о том, что центр масс предмета можно переместить какими-то манипуляциями внутри него. Он считал, что никакие внутренние действия не могут изменить центр масс. Но если это так, то при перемещении энергии U с одного конца на другой сам вагон должен откатиться на расстояние х (фиг. 27.7, в ). В самом деле, нетрудно убедиться, что полная масса вагона, умноженная на х , должна быть равна произведению перемещенной энергии U / c 2на длину L (при условии, что U / c 2много меньше М ), т . е.

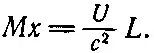(27.22)

Теперь рассмотрим конкретный случай, когда энергия переносится вспышкой света. (Все рассуждения можно повторить и для частиц, но мы будем следовать за Эйнштейном, который интересовался проблемами света.) Что заставляет вагон двигаться? Эйнштейн рассуждал так: при испускании света должна быть отдача, какая-то неизвестная отдача с импульсом р . Именно она заставляет вагон откатиться назад. Скорость вагона v при такой отдаче должна быть равна импульсу отдачи, поделенному на массу М :

Вагон движется с этой скоростью до тех пор, пока свет не достигнет противоположного конца. Ударяясь, свет отдает импульс вагону и останавливает его. Если х мало, то время, в течение которого вагон движется, равно L / c , так что мы получаем

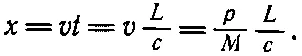
Подставляя х в (27.22), находим

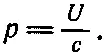
Снова получилось соотношение между энергией и импульсом света. Деля это на с , находим плотность импульса g = p / c , и опять

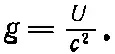(27.23)