Ричард Фейнман - Том 2. Электромагнетизм и материя

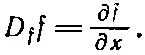
Но если мы имеем выражение D f fg , то оно означает

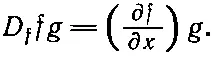
Заметим теперь, что, согласно нашему новому правилу, fD f g означает то же самое. Одно и то же выражение можно записать любым из следующих способов:

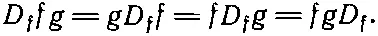
Вы видите, что D f может стоять даже после всего. (Странно, почему такому удобному обозначению обычно не учат в книгах по математике и физике.)

Вы, пожалуй, удивитесь: а что, если я хочу написать производную от fg ? Если мне нужна производная от обоих членов? Это очень легко: вы пишете D f ( fg )+ D g ( fg ), т.e. g (∂ f /∂ x )+ f (∂ g /∂ x ), что в старых обозначениях как раз равно ∂( fg )/∂ x .

Вы сейчас увидите, как просто теперь получить новое выражение для ∇·( В× E). Начнем с перехода к новому обозначению и напишем

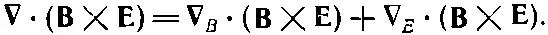(27.10)

Как только мы сделали это, уже нет больше нужды придерживаться строгого порядка. Мы всегда знаем, что ∇ E действует только на Е, а ∇ B действует только на В. При этих обстоятельствах оператором ∇можно пользоваться как обычным вектором. (Разумеется, после того как все будет окончено, нам захочется вернуться к «стандартным» обозначениям, которые обычно используются.) Таким образом, теперь мы можем делать различные перестановки сомножителей. Так, средний сомножитель в уравнении (27.10) можно переписать как Е·( ∇ B × B). [Надеюсь, вы помните, что a·( b× c)= b·( c× a).] А последний — как В·( E× ∇ E ). Хотя это выглядит несколько странно, но тем не менее здесь все в порядке. Если же мы теперь попытаемся вернуться к старым обозначениям, то должны будем расположить операторы ∇так, чтобы они действовали на свои «собственные» переменные. В первом из них все в порядке, так что мы можем просто опустить индекс у ∇. Второй же требует некоторой реорганизации, чтобы оператор ∇поставить перед Е. Этого можно добиться, переставляя сомножители в векторном произведении и меняя знак:

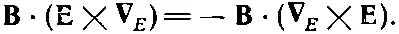
Теперь все стоит на своем месте и можно вернуться к обычным обозначениям. Формула (27.10) эквивалентна следующему равенству:

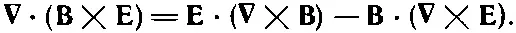(27.11)

(В этом специальном случае быстрее было бы использовать компоненты, но, право же, стоило потратить время ради того, чтобы показать вам математический трюк. Может случиться, что вы больше нигде его не встретите, а он очень удобен тогда, когда в векторной алгебре нужно освободиться от правила порядка членов при дифференцировании.)

Вернемся теперь к нашему закону сохранения энергии, причем для преобразования ∇× Bв (27.7) мы используем новый результат — равенство (27.11). Вот что оно дает:

(27.12)

Теперь вы видите, что мы почти у цели. Одно из наших слагаемых — настоящая производная по t , ее мы используем при образовании и , а другое (превосходная дивергенция) войдет в S. К несчастью, справа в середине осталось еще одно слагаемое, которое не является ни дивергенцией, ни производной по t . Так что пока еще не все закончено. После некоторых размышлений мы опять обращаемся к уравнениям Максвелла и, к счастью, обнаруживаем, что (∇× E) равно —∂ B/∂ t .

Это позволяет превратить дополнительный член в чистую производную чего-то по времени:

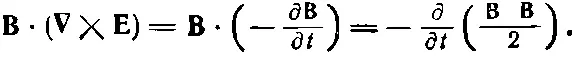
Вот теперь у нас получилось то, что нужно. Уравнение для энергии переписывается в виде

(27.13)

А это, если мы определим u и Sкак

(27.14)

и

(27.15)

в точности напоминает уравнение (27.6). (Перестановкой сомножителей в векторном произведении мы добиваемся правильного знака.)

Итак, наша программа успешно выполнена. Из выражения для плотности энергии мы видим, что она представляет сумму «электрической» и «магнитной» плотностей энергии, которые в точности равны выражениям, полученным нами в статике, когда мы находили выражение для энергии через поля . Кроме того, мы получили выражение для вектора потока энергии электромагнитного поля. Этот новый вектор S=ε 0c 2 E× Bпо имени своего первооткрывателя называется «вектором Пойнтинга». Он говорит нам о скорости, с которой энергия движется в пространстве. Энергия, протекающая в секунду через малую поверхность da , равна S· n da , где n— вектор, перпендикулярный к поверхности da . (Теперь, когда у нас есть формулы для u и S, можете, если хотите, забыть все выкладки.)

Прежде чем заняться некоторыми приложениями формул Пойнтинга [т. е. выражений (27.14) и (27.15)], я хотел бы заметить, что на самом деле мы их не «доказали». Все, что мы сделали,— это нашли только возможное u и возможное S. Но откуда же нам известно, что, покрутив формулами, мы не придем к другому выражению для u и другому выражению для S? Новое Sи новое и будут отличаться от старых, но по-прежнему будут удовлетворять уравнению (27.6). Такое вполне может случиться. Однако в формулы, которые получаются при этом, всегда входят различные производные полей (причем это всегда члены второго порядка типа второй производной или квадрата первой производной). Для u и Sможно фактически написать бесконечное число различных выражений, и до сих пор никто не думал над экспериментальной проверкой того, которое же из них истинное. Люди полагают, что простейшее выражение, по-видимому, и должно быть истинным, но надо сознаться, что мы так и не знаем, как же на самом деле распределена энергия в электромагнитном поле. Пойдем по тому же легчайшему пути и постулируем, что энергия поля определяется выражением (27.14). При этом вектор потока Sдолжен задаваться уравнением (27.15).