Ричард Фейнман - Том 2. Электромагнетизм и материя

Раньше мы видели, что над каждой единицей объема вещества поле в единицу времени производит работу Е·j. [Сила, действующая на частицу, равна F=q( E+ v× B), а мощность равна F·v=q E· v. Если в единице объема содержится N частиц, то эта мощность в единице объема равна Nq E·v, а Nq v= j.] Таким образом, величина Е·jдолжна быть равна энергии, теряемой полем в единице объема за единицу времени. Уравнение (27.3) при этом приобретает вид

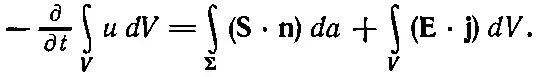(27.4)

Вот как выглядит наш закон сохранения энергии в поле. Его можно записать как дифференциальное уравнение, подобное (27.2); для этого второе слагаемое нужно превратить в интеграл по объему, что легко делается с помощью теоремы Гаусса. Поверхностный интеграл от нормальной компоненты Sравен интегралу от дивергенции Sпо объему, ограниченному этой поверхностью, так что уравнение (27.3) эквивалентно следующему:

где производную по времени от первого слагаемого мы внесли под интеграл. Поскольку это уравнение верно для любого объема, то интегралы можно отбросить и получить уравнение для энергии электромагнитного поля:

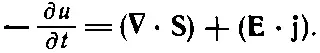(27.5)

Однако это уравнение не даст нам ничего хорошего, пока мы не узнаем, что такое u и S. Быть может, мне следовало бы просто сказать вам, как они выражаются через Еи В, поскольку это единственное, что нам, собственно, нужно. Однако мне очень хочется изложить вам все те рассуждения, которыми в 1884 г. воспользовался Пойнтинг, чтобы получить формулы для Sи u , с тем, чтобы вы понимали, откуда они взялись. (Для дальнейшей работы, впрочем, вам этот вывод не потребуется.)

Идея заключается в том, что должны существовать плотность энергии u и поток S, которые зависят только от полей Еи В. [В электростатике, например, плотность энергии, как мы знаем, можно записать в виде 1/ 2ε 0( Е· Е).] Разумеется, u и Sмогут зависеть от потенциалов и чего-то другого, но давайте лучше посмотрим, что мы можем написать. Попытаемся переписать величину Е· jв таком виде, чтобы она стала суммой двух слагаемых, одно из которых было бы производной по времени от некоторой величины, а второе — дивергенцией. Тогда первую величину мы бы назвали и, а вторую — S(разумеется, с надлежащими знаками). Обе величины должны быть выражены только через поля, т. е. мы хотим записать наше равенство в виде

(27.6)

причем левая часть уравнения должна выражаться только через поля. Как это сделать? Разумеется, нужно воспользоваться уравнениями Максвелла. Из уравнения для ротора Вимеем

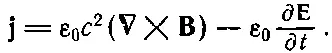
Подставляя это в (27.6), получаем выражение его только через Еи В:

(27.7)

Работа частично нами уже закончена. Последнее слагаемое есть производная по времени — это (∂/∂ t )( 1/ 2ε 0 Е· Е).

Итак, 1/ 2ε 0 Е· Едолжно быть по крайней мере частью u . Такое же выражение получалось у нас и в электростатике. А теперь единственное, что нам остается сделать,— это превратить в дивергенцию чего-то второе слагаемое.

Заметьте, что первое слагаемое в правой части (27.7) переписывается в виде

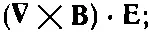(27.8)

вы знаете из векторной алгебры, что ( a× b)· cравно а·( b× c), поэтому первое слагаемое принимает вид

(27.9)

т. е. получилась дивергенция «чего-то», к которой мы так стремились. Получилась, но только все это неверно! Я предупреждал вас, что оператор ∇только «похож» на вектор, а на самом деле он не «настоящий» вектор. Вспомните, что в дифференциальном исчислении существует дополнительное соглашение : когда оператор производной стоит перед произведением, он действует на все стоящее правее него. Вуравнении (27.7) оператор ∇действует только на Ви не затрагивает Е. Но если бы мы записали его в форме уравнения (27.9), то общепринятое соглашение говорило бы, что ∇действует как на В, так и на Е. Так что это не одно и то же . В самом деле, если расписать ∇·( В× E) по компонентам, то можно убедиться, что оно равно E·( ∇× B) плюс какие-то другие слагаемые. Это напоминает взятие производной от произведения в обычном анализе. Например,

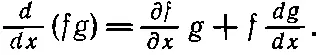
Вместо того чтобы выписать все компоненты ∇·( B× E), мне бы хотелось показать вам один трюк, очень полезный в задачах такого рода. Он позволит вам всюду в выражениях, содержащих оператор ∇, пользоваться правилами векторной алгебры, не попадая впросак. Трюк состоит в отбрасывании (по крайней мере на время) правил дифференциального исчисления относительно того, на что действует оператор производной. Вы знаете, что порядок сомножителей важен в двух различных случаях. Во-первых, в дифференциальном исчислении: f ( d / dx ) g не то же самое, что g ( d / dx ) f ; и, во-вторых, в векторной алгебре: a× bотличается от b× а. Мы можем, если захотим, на минуту отказаться от правил дифференциального исчисления. Вместо того чтобы говорить, что производная действует на все стоящее правее от нее, мы примем новое правило, избавляющее нас от порядка, в котором записаны сомножители. После этого мы можем крутить ими, как хотим, без всяких помех.

Вот наше новое правило: с помощью индекса мы будем указывать, на что же именно действует дифференциальный оператор; при этом порядок сомножителей не имеет никакого значения. Допустим, что оператор ∂/∂ x мы обозначили через D . Тогда символ D f говорит, что берется производная только функции f , т. е.