Ричард Фейнман - Том 2. Электромагнетизм и материя

Для движущейся частицы ds легко связывается с dt . Для точечной частицы

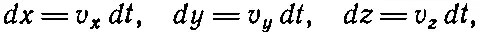(26.30)

а

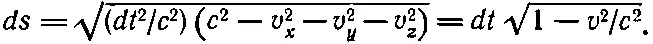(26.31)

Таким образом, оператор

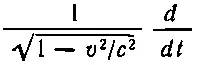
есть инвариантный оператор . Если подействовать им на любой четырехвектор, то мы получим другой четырехвектор. Например, если мы действуем им на ( ct, x, у, z ), то получаем четырехвектор скорости

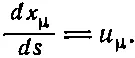
Теперь мы видим, почему √(1- v 2/ c 2) поправляет дело.

Инвариантная переменная s — очень полезная физическая величина. Ее называют «собственным временем» вдоль траектории частицы, ибо в системе, в любой момент движущейся вместе с частицей, ds просто равно интервалу времени. (В этой системе Δx=Δy=Δz=0, а Δs=Δt.) Если вы представите себе часы, скорость хода которых не зависит от ускорения, то, двигаясь вместе с частицей, такие часы будут показывать время s.

Теперь можно вернуться назад и записать закон Ньютона (подправленный Эйнштейном) в изящной форме:

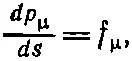(26.32)

где f μопределяется формулой (26.28). Импульс же р μможет быть записан в виде

(26.33)

где координаты x μ=( ct, х, у, z ) описывают теперь траекторию частицы. Наконец, четырехмерные обозначения приводят нас к очень простой форме уравнений движения:

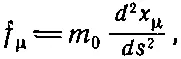(26.34)

напоминающей уравнения F= m a. Важно отметить, что уравнения (26.34) и F= m a— вещи разные, ибо четырехвекторная форма уравнения (26.34) содержит в себе релятивистскую механику, которая при больших скоростях отличается от механики Ньютона. Это абсолютно непохоже на случай уравнений Максвелла, где нам нужно был о переписать уравнения в релятивистской форме, совершенно не изменяя их смысла , а изменяя лишь обозначения.

Вернемся теперь к уравнению (26.24) и посмотрим, как в четырехвекторных обозначениях записывается правая часть. Три компоненты F, поделенные на √(1-v 2/c 2), составляют пространственные компоненты f μ, так что

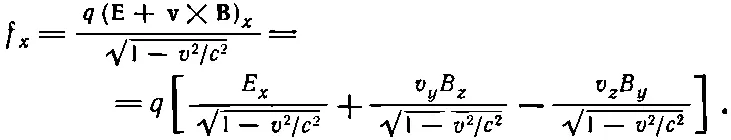(26.35)

Теперь мы должны подставить все величины в их релятивистских обозначениях. Прежде всего c/√(1- v 2/ c 2), v y /√(1- v 2/ c 2) и v z /√(1- v 2/ c 2) представляют t -, у - и z-компоненты 4-скорости u μ. Компоненты же Еи Ввходят в электромагнитный тензор второго ранга F μ v . Отыскав в табл. 26.1 компоненты F μ v , соответствующие Е х , В z и В y , получим

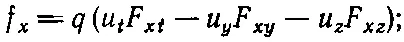
здесь уже начинает вырисовываться что-то интересное. В каждом слагаемом есть индекс х , и это разумно, ибо мы находим х-компоненту силы. Все же остальные индексы появляются в парах tt, yy, zz — все, кроме слагаемого с хх , которое куда-то делось. Давайте просто вставим его и запишем

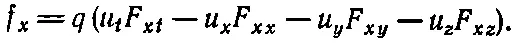(26.36)

Этим мы ничего не изменили, так как благодаря антисимметрии F μ v слагаемое F xx равно нулю. Причиной же нашего желания восстановить его является возможность сокращенной записи уравнения (26.36):

(26.37)

Это по-прежнему уравнение (26.36), если предварительно мы примем соглашение : когда какой-то индекс встречается в произведении дважды (подобно v), нужно автоматически суммировать все слагаемые с одинаковыми значениями этого индекса точно так же, как и в скалярном произведении, т. е. пользуясь тем же самым правилом знаков .

Нетрудно поверить, что уравнение (26.37) так же хорошо работает и для μ=y, и для μ= z . Но как обстоит дело с μ=t? Посмотрим для забавы, что дает формула

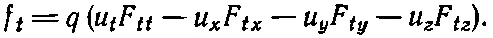
Теперь мы снова должны перейти к Еи В. После этого получается

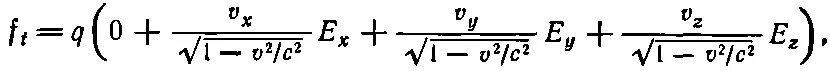(26.38)

или

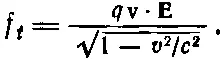
Но в (26.28) f t бралось равным

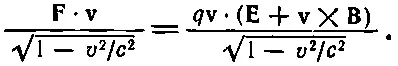
А это одно и то же, что (26.38), ибо v·( v× B) равно нулю. Так что все идет как нельзя лучше.

В результате наше уравнение движения записывается в элегантном виде:

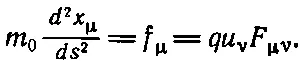(26.39)

Как ни приятно видеть столь красиво записанное уравнение, форма эта не особенно полезна. При нахождении движения частицы обычно удобнее пользоваться первоначальным уравнением (26.24), что мы и будем делать в дальнейшем.

То, что энергия вещества не всегда сохраняется, ясно как день. При излучении света объект теряет энергию. Однако потерянную энергию можно представить в какой-то другой форме, скажем, в форме энергии света. Поэтому закон сохранения энергии не полон, если не рассмотреть энергию, связанную со светом, в частности, и с электромагнитным полем вообще. Сейчас мы подправим его, а заодно и закон сохранения импульса с учетом электромагнитного поля. Мы, разумеется, не можем обсуждать их порознь, ибо, согласно теории относительности, это различные проявления одного и того же четырехвектора.

С сохранением энергии мы познакомились еще в начале нашего курса; тогда мы просто сказали, что полная энергия в мире остается постоянной. Теперь же мы хотим сделать очень важное обобщение идеи закона сохранения энергии, которое скажет нам нечто о деталях того, как это происходит. Новый закон будет говорить, что если энергия уходит из какой-то области, то это может происходить только за счет ее вытекания через границы рассматриваемой области. Это утверждение сильнее, чем просто сохранение энергии без подобных ограничений.