Ричард Фейнман - Том 2. Электромагнетизм и материя

Итак, единственное, что мы должны сделать для определения скорости v ,— это измерить напряжение между концами провода. Хотя для этой цели мы не можем воспользоваться вольтметром, ибо то же самое поле будет действовать и на провода внутри вольтметра, способы измерения таких полей все же существуют. О некоторых из них мы уже говорили в гл. 9 (вып. 5), когда рассказывали об атмосферном электричестве. Так что измерить скорость самолета, казалось бы, можно.

Однако эта важная проблема не была решена таким методом. Дело в том, что величина электрического поля, которое при этом развивается,— порядка нескольких милливольт на метр. Измерить такие поля, конечно, можно, но вся беда в том, что они ничем не отличаются от любых других электрических полей. Поля, создаваемые движением через магнитное поле, нельзя отличить от электрических полей, возникающих в воздухе по каким-то другим причинам (скажем, от электростатических зарядов в воздухе или на облаках). В гл. 9 мы говорили, что обычно над поверхностью Земли существуют электрические поля с напряженностью около 100 в / м , но они совершенно нерегулярные. Так что самолет во время полета будет наблюдать флуктуации атмосферных электрических полей, которые огромны по сравнению со слабенькими полями, возникающими из-за множителя v× B. Ввиду этих чисто практических причин измерить скорость самолета, используя его движение в магнитном поле Земли, невозможно.

Полученные из уравнений Максвелла электрические и магнитные поля сами по себе не представляют особой ценности, если мы не знаем, что эти поля могут делать, на что они способны. Вы, вероятно, помните, что поля нужны для нахождения действующих на заряды сил и что именно эти силы определяют их движение. Так что связь движения зарядов с силами, разумеется, тоже есть часть электродинамики.

На отдельный заряд, находящийся в полях Еи В, действует сила

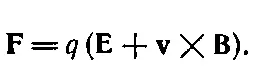(26.23)

При небольших скоростях эта сила равна произведению массы на ускорение, но истинный закон, справедливый при любых скоростях, гласит: сила равна dp / dt . Подставляя p = m 0 v /√(1- v 2/c 2), находим релятивистское уравнение движения заряда:

(26.24)

Теперь мы хотим обсудить это уравнение с точки зрения теории относительности. Поскольку уравнения Максвелла записаны у нас в релятивистской форме, интересно посмотреть, как в релятивистской же форме выглядят уравнения движения. Посмотрим, можно ли переписать уравнения движения в четырехмерных обозначениях.

Мы знаем, что импульс есть часть четырехмерного вектора p μс энергией m 0/√(1- v 2/с 2) в качестве временной компоненты, так что мы надеемся заменить левую часть уравнения (26.24) на dp μ/ dt . Теперь нам нужно найти только четвертую компоненту силы F. Эта компонента должна быть равна скорости изменения энергии или скорости совершения работы, т. е. F· v. Так что правую часть уравнения (26.24) желательно было бы записать в виде четырехвектора типа ( F· v, F x , F y , F z ). Однако эти величины не составляют четырехвектора.

Производная четырехвектора по времени не будет больше четырехвектором, так как d / dt требует для измерения t некоторой специальной системы отсчета. С этой трудностью мы уже сталкивались раньше, когда пытались сделать четырехвектор из скорости v. Тогда мы попытались считать, что роль временной компоненты скорости играет cdt / dt = c . Но на самом деле величины

(26.25)

не образуют четырехвектора. После этого мы обнаружили, что их можно превратить в компоненты четырехвектора, если помножить каждую на 1/√(1-v 2/ с 2). «Четырехмерной скоростью» u μоказался вектор

(26.26)

Вот в чем фокус! Нужно умножать производную d / dt на 1/√(1- v 2/с 2), если мы хотим превратить ее компоненту в четырехвектор.

Итак, вторая гипотеза: четырехвектором должна быть величина

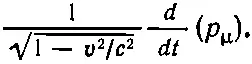(26.27)

Но что такое v? Это уже скорость частицы, а не скорость системы координат! Таким образом, обобщением силы на четырехмерное пространство будет величина f μ:

(26.28)

которую мы назовем «4-силой». Она уже четырехвектор, и ее пространственными компонентами будут уже не F, а F/√(1-v 2/c 2).

Почему же f μчетырехвектор? Неплохо бы понять, что это за таинственный множитель 1/√(1-v 2/с 2). Так как мы встречаемся с ним уже второй раз, то самое время посмотреть, почему производная d / dt всегда должна входить с одним и тем же множителем. Ответ заключается вот в чем. Когда мы берем производную по времени некоторой функции х , то подсчитываем приращение Δ х за малый интервал Δ t переменной t . Но в другой системе отсчета интервал Δ t может соответствовать изменению как t ', так и х ', так что при изменении только t ' изменение х будет другим. Для наших дифференцирований следовало бы найти такую переменную, которая была бы мерой «интервала» в пространстве - времени и оставалась бы той же самой во всех системах отсчета. Когда в качестве этого интервала мы принимаем приращение Δ х , то оно будет тем же во всех системах отсчета. Когда частица «движется» в четырехмерном пространстве, то возникают приращения как Δ t , так и Δ х , Δ y , Δ z . Можно ли из них сделать интервал? Да, они образуют компоненты приращения четырехвектора х μ=( сt, х, у, z ), так что, если определить величину Δs через

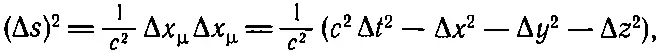(26.29)

что представляет четырехмерное скалярное произведение, то в ней мы приобретаем настоящий скаляр и можем пользоваться им для измерения четырехмерного интервала. Исходя из величины Δs или ее предела ds , мы можем определить параметр s =∫ ds . Хорошим четырехмерным оператором будет и производная по s, т . е. d / ds , так как она инвариантна относительно преобразований Лоренца.