Ричард Фейнман - Том 2. Электромагнетизм и материя

(26.20)

(Для наших целей а м следует, в конце концов, заменить на ∇ μ, а b μ—на потенциал А μ.) Компоненты а μи b μпреобразуются по формулам Лоренца:

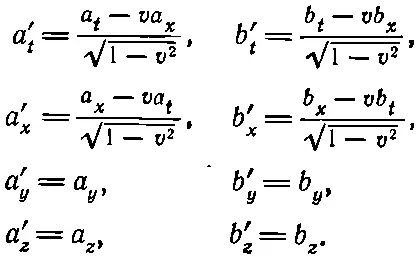(26.21)

Теперь преобразуем компоненты G μv. Начнем с G tx :

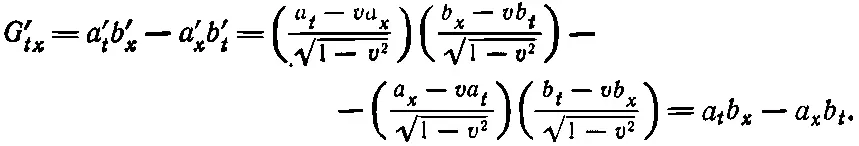
Но ведь это просто G tx . Таким образом, мы получили простой результат

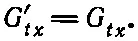
Возьмем еще одну компоненту:

Итак, получается

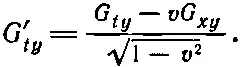
И, конечно, точно таким же образом

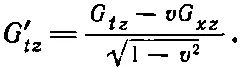
А теперь ясно, как ведут себя все остальные компоненты. Давайте составим таблицу преобразований всех шести членов; только теперь мы будем все писать для величин F μ v :

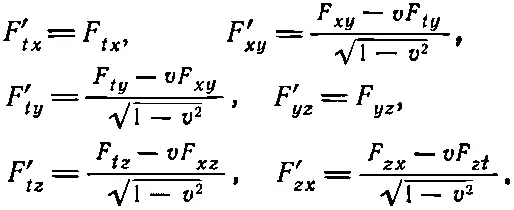(26.22)

Разумеется, по-прежнему у нас F ' μ v =— F ' μ v , а F ' μμ=0.

Итак, мы имеем преобразования электрических и магнитных полей. Единственное, что нам нужно сделать,— это заглянуть в табл. 26.1 и узнать, что означает для векторов Е и В преобразование, записанное для F μ v . Речь идет о простой подстановке. Чтобы можно было видеть, как это все выглядит в обычных символах, перепишем наши преобразования компонент поля в виде табл. 26.2.

Таблица 26.2. ЛОРЕНЦЕВЫ ПРЕОБРАЗОВАНИЯ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЕЙ

Уравнения в этой таблице говорят нам, как изменяются Еи Впри переходе от одной инерциальной системы к другой. Если известны Еи Вв одной системе, то мы можем найти, чему они равны в другой, движущейся относительно нее со скоростью v .

Можно переписать эти уравнения в форме, более легкой для запоминания. Для этого заметьте, что поскольку скорость v направлена по оси х , то все компоненты с v представляют собой векторные произведения v× Eи v× B. Так что преобразования можно записать в виде табл. 26.3.

Таблица 26.3. ДРУГАЯ ФОРМА ПРЕОБРАЗОВАНИЯ ПОЛЕЙ

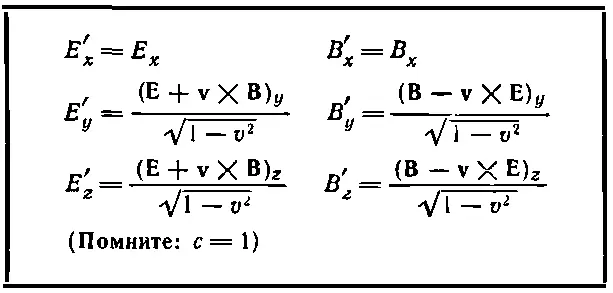
Теперь легко запомнить, какая компонента куда идет. Фактически эти преобразования можно записать даже еще проще, если ввести компоненты поля, направленные по оси х , т. е. «параллельные» компоненты E ║и В ║(которые параллельны относительной скорости систем S и S') и полные поперечные или «перпендикулярные» компоненты Е ┴ и В ┴, т. е. векторную сумму у - и z-компонент. В результате мы получим уравнения, сведенные в табл. 26.4. (Для полноты мы восстановили все с .)

Таблица 26.4. ЕЩЕ ОДНА ФОРМА ЛОРЕНЦЕВЫХ ПРЕОБРАЗОВАНИЙ ПОЛЕЙ ЕИ В

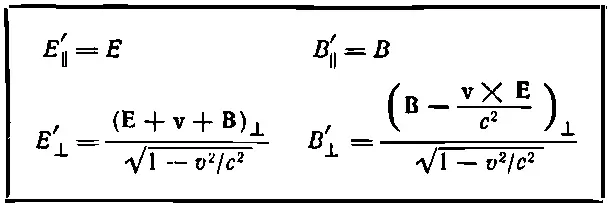
Преобразования поля позволяют по-другому решить задачи, которыми мы занимались прежде, например найти поле движущегося точечного заряда. Раньше мы вычисляли поля, дифференцируя потенциалы. Но теперь то же самое можно сделать, преобразуя кулоново поле. Если у нас в системе S находится покоящийся заряд, то он создает только простое радиальное поле Е. В системе S ', движущейся относительно системы S со скоростью v =-u, точечный заряд будет казаться нам летящим со скоростью и . Покажите сами, что преобразования табл. 26.3 и 26.4 дают те же самые электрические и магнитные поля, которые мы получили в § 2.

Преобразования табл. 26.2 дают нам очень интересный и простой ответ на вопрос: что мы видим, если движемся мимо любой системы фиксированных зарядов? Пусть нам хочется узнать поля в нашей системе S ', если мы движемся между пластинами конденсатора вдоль него, как показано на фиг. 26.7. (Но, разумеется, все равно, если бы заряженный конденсатор двигался мимо нас .)

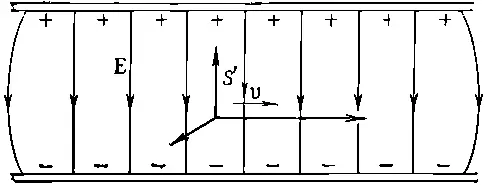
Фиг. 26.7. Система координат S' движется в статическом электрическом поле.

Что же мы увидим? Преобразования в этом случае облегчаются тем, что в первоначальной системе поле Вотсутствует. Предположим сначала, что наше движение перпендикулярно к направлению Е, при этом мы увидим поле Е'= Е/√(1- v 2/ с 2), которое остается полностью поперечным. Но мы еще увидим и магнитное поле В'=- v× E'/ c 2. (He удивляйтесь, что в этой формуле нет √(1- v 2); ведь мы записали ее через Е', а не через Е; так тоже можно делать.) Итак, когда мы движемся в направлении, перпендикулярном к статическому полю, то видим измененное Еи вдобавок еще поперечное поле В. Если наше движение не перпендикулярно вектору Е, то мы разбиваем Ена Е ║и Е ┴. Параллельная часть остается неизменной, E' ║= E ║, а что происходит с перпендикулярной компонентой, мы уже описали.

Давайте разберем противоположный случай и вообразим, что мы движемся через чисто статическое магнитное поле. На этот раз мы бы увидели электрическое поле Е', равное v× B', и магнитное поле, усиленное множителем 1/√(1- v 2/ с 2) (предполагая, что оно поперечное). До тех пор, пока v много меньше с , изменением магнитного поля можно пренебречь, и основным эффектом будет появление электрического поля. В качестве примера этого эффекта рассмотрим некогда знаменитую проблему определения скорости самолета. Сейчас она уже больше не знаменита, поскольку для определения скорости можно использовать отражение от Земли сигналов радиолокатора. Но раньше в плохую погоду скорость самолета было очень трудно определить. Ведь вы не видите Землю и не можете сказать куда вы летите. А знать, насколько быстро вы движетесь относительно Земли, было важно. Как же это можно сделать, не видя ее? Те, кому были знакомы уравнения преобразования, считали, что нужно использовать тот факт, что самолет движется в магнитном поле Земли. Предположим, что самолет летит там, где магнитное поле нам более или менее известно. Возьмем простейший случай, когда магнитное поле вертикально. Если мы летим через него с горизонтальной скоростью v , то в соответствии с нашей формулой должны наблюдать электрическое поле v× B, т. е. перпендикулярное к направлению движения. Если поперек самолета подвесить изолированный провод, то электрическое поле на его концах будет индуцировать заряды. Ну в этом ничего нового нет. С точки зрения наблюдателя на Земле, мы просто передвигаем провод в магнитном поле, а сила q ( v× B) заставляет заряд двигаться к концу провода. Уравнения преобразования говорят то же самое, но другими словами. (То, что одну и ту же вещь можно получить не одним, а несколькими способами, вовсе не означает, что один способ лучше другого. Мы овладели столькими методами и приемами, что один и тот же результат можем получать какими хотите способами!)