Ричард Фейнман - Том 2. Электромагнетизм и материя

Аналогично,

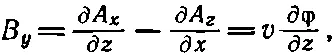
или

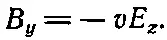(26.8)

Наконец, компонента В х равна нулю, поскольку равны нулю и А у и А z . Таким образом, магнитное поле можно записать в виде

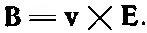(26.9)

Теперь посмотрим, как выглядят наши поля. Мы попытаемся нарисовать картину поля вокруг положения заряда в настоящий момент. Конечно, влияние заряда в каком-то смысле происходит из запаздывающего положения, но, поскольку мы имеем дело со строго заданным движением, запаздывающее положение однозначно определяется положением в настоящий момент. При постоянной скорости заряда поля лучше связывать с текущими координатами, ибо компоненты поля в точке х, у, z зависят только от ( х - vt ), у и z, которые являются компонентами вектора перемещения r p из постоянного положения заряда в точку ( х, у, z ) (фиг. 26.3).

Фиг. 26.3. Электрическое поле заряда, движущегося с постоянной скоростью, направлено по радиусу от истинного положения заряда.

Рассмотрим сначала точки, для которых z=0. Поле Ев этих точках имеет только х - и y -компоненты. Из уравнений (26.3) и (26.6) видно, что отношение этих компонент как раз равно отношению х - и y -компонент вектора перемещения. Это означает, что направление Е совпадает с направлением r p , как это показано на фиг. 26.3. Тот же результат остается справедливым и для трех измерений, поскольку E z пропорционально z. Короче говоря, электрическое поле заряда радиально и силовые линии расходятся от заряда так же, как и в стационарном случае. Конечно, вследствие наличия дополнительного фактора (1-v 2) поле не будет тем же самым, что в стационарном случае. Но здесь мы можем увидеть нечто очень интересное. Дело обстоит так, как будто вы пишете закон Кулона в особой системе координат, «сжатой» вдоль оси x множителем √(1-v 2). Если вы сделаете это, то силовые линии впереди и позади заряда разойдутся, а по бокам сгустятся (фиг. 26.4).

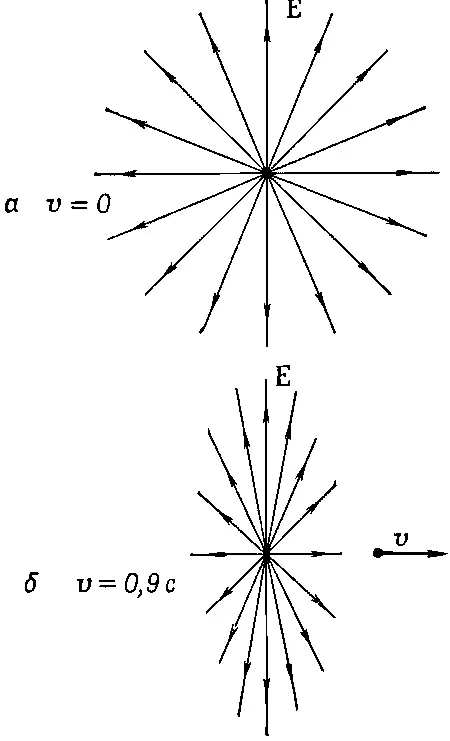
Фиг .26.4. Электрическое поле заряда. а — неподвижного, б — летящего с постоянной скоростью v=0,9 с.

Если мы связываем обычным образом напряженность поля Ес плотностью силовых линий, то видим, что поле впереди и позади заряда ослабевает, но зато по бокам становится сильнее, т. е. как раз то, о чем говорит нам уравнение. Когда вы измеряете напряженность поля под прямыми углами к линии движения, т. е. при ( x - vt )=0, расстояние от заряда будет равно y 2+z 2, а полная напряженность √( E z 2+ E y 2) в этих точках равна

(26.10)

Она, как и в случае кулонова поля, пропорциональна квадрату расстояния, но еще усиливается постоянным множителем 1/√(1-v 2), который всегда больше единицы. Таким образом, по бокам движущегося заряда электрическое поле сильнее, чем это следует из закона Кулона. Фактически увеличение по сравнению с кулоновым потенциалом равно отношению энергии частицы к ее массе покоя.

Впереди заряда (или позади него) у и z равны нулю, а поэтому

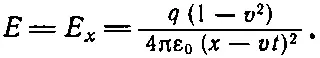(26.11)

Снова поле обратно пропорционально расстоянию от заряда, но теперь оно зарезается множителем (1- v 2), что согласуется с картиной силовых линий. Если v / c мало, то v 2/ c 2еще меньше, и действие (1- v 2) почти незаметно, поэтому мы снова возвращаемся к закону Кулона. Но если частица движется со скоростью, близкой к скорости света, то поле перед частицей сильно уменьшается, а поле сбоку чудовищно возрастает.

Наш результат, относящийся к электрическому полю заряда, можно представить и так. Предположим, что вы на клочке бумаги нарисовали силовые линии покоящегося заряда, а затем эту картину запустили со скоростью v 2. Тогда благодаря лоренцеву сокращению рисунок сожмется, т. е. частички графита на бумаге будут казаться нам расположенными в других местах. Но чудо состоит в том, что в результате на пролетающем мимо листочке вы увидите точную картину силовых линий точечного движущегося заряда. Лоренцево сокращение сблизит их по бокам, раздвинет перед зарядом и позади него как раз настолько, чтобы получить нужную плотность. Мы уже отмечали, что силовые линии — это не реальность, а лишь способ представить себе электрическое поле. Однако здесь они ведут себя как самые настоящие реальные линии. В этом частном случае, если вы и сделали ошибку, рассматривая силовые линии как нечто реальное и преобразуя их как реальные линии в пространстве, поле в результате все равно получилось бы правильным. Однако от этого силовые линии не станут более реальными. Вспомните об электрическом поле, создаваемом зарядом вместе с магнитом; когда магнит движется, он создает новое электрическое поле и разрушает всю нашу прекрасную картину. Так что простая идея сокращающейся картинки, вообще говоря, не годится. Но все же это очень удобный способ запомнить, как выглядит поле быстро движущегося заряда.

Магнитное поле [из уравнения (26.9)] равно v× E. Когда вы векторно помножите скорость на радиальное поле Е, то получите поле В, силовые линии которого представляют окружности вокруг линии движения (фиг. 26.5).

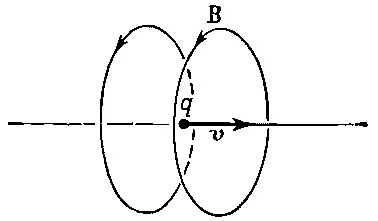
Фиг. 26.5. Магнитное поле вблизи движущегося заряда равно v×E (ср. с фиг. 26.4).

Если же теперь мы подставим обратно все с , то вы убедитесь, что результат получился тот же, что и для медленно движущихся зарядов. Хороший способ установить, куда должны войти с , — это вспомнить формулу для силы:

Вы видите, что произведение скорости на магнитное поле имеет ту же размерность, что и электрическое поле, так что в правой части (26.9) должен стоять множитель 1/с 2, т. е.

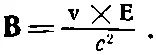(26.12)