Ричард Фейнман - Том 2. Электромагнетизм и материя

(25.21)

С правой стороны (25.21) стоят четыре величины ρ, j x , j, j z , поделенные на ε 0— универсальную постоянную, одинаковую во всех системах координат, если во всех системах для измерения заряда используется одна и та же единица. Таким образом, четыре величины ρ/jе 0, j х/ε 0, j y/ε 0, j z/ε 0тоже преобразуются как четырехвектор. Их можно записать в виде j μ s /е 0. Оператор Даламбера не изменяется при переходе к другим системам координат, так что четыре величины φ, А х , А у и A z тоже должны преобразоваться как четырехвектор, т. е. должны быть компонентами четырехвектора. Короче говоря, величина

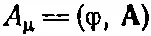
есть четырехвектор. То, что мы называли скалярным и векторным потенциалами, оказывается только разными частями от одной и той же физической величины. Они неотделимы друг от друга. А если это так, то релятивистская инвариантность мира очевидна. Вектор А μмы называем четырехмерным потенциалом (4-потенциалом).

В четырехмерных обозначениях (25.21) приобретает очень простой вид:

(25.22)

Физика этого уравнения та же, что и уравнений Максвелла. Но есть своя прелесть в том, что можно переписывать их в столь элегантной форме. Впрочем, эта красивая форма содержит и кое-что более значительное — из нее непосредственно видна инвариантность электродинамики относительно преобразований Лоренца.

Напомним, что уравнение (25.21) можно получить из уравнений Максвелла только тогда, когда наложено дополнительное условие градиентной инвариантности:

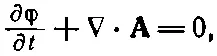(25.23)

что означает просто ∇μAμ=0, т. е. условие градиентной инвариантности говорит, что дивергенция четырехмерного вектора Аμ равна нулю. Это требование носит название условия Лоренца . Такая форма его записи очень удобна, ибо она инвариантна, а поэтому уравнения Максвелла во всех системах отсчета сохраняют вид (25.22).

Теперь выпишем законы преобразования, выражающие φ и Ав движущейся системе через φ и Ав неподвижной, хотя неявно мы уже говорили о них. Поскольку А μ=(φ, А) является четырехвектором, это уравнение должно выглядеть подобно (25.1), за исключением того, что t нужно заменить на φ, а x— на А. Таким образом,

(25.24)

При этом предполагается, что штрихованная система координат движется по отношению к нештрихованной со скоростью v в направлении оси х .

Рассмотрим один пример плодотворности идеи 4-потенциала. Чему равны векторный и скалярный потенциалы заряда q , движущегося со скоростью v в направлении оси х ? Задача очень упрощается в системе координат, движущейся вместе с зарядом, ибо в этой системе заряд покоится. Пусть заряд находится в начале координат системы S ', как это показано на фиг. 25.2.

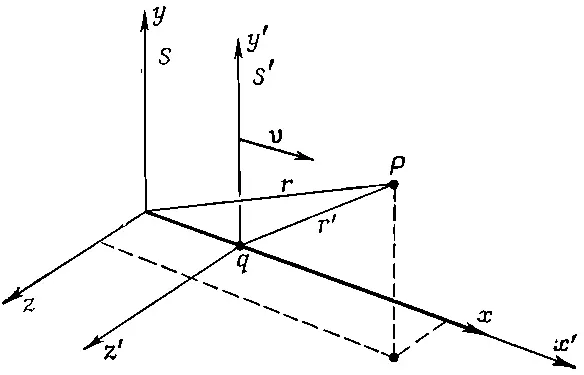
Фиг. 25.2. Система отсчета S' движется со скоростью v (в направлении оси х) по отношению к системе S. Заряд, покоящийся в начале системы координат S', находится в системе S в точке x=vt. Потенциалы в точке Р могут быть найдены для любой системы отсчета.

Скалярный потенциал в движущейся системе задается выражением

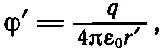(25.25)

причем r' — расстояние от заряда q до точки в движущейся системе, где производится измерение поля. Векторный же потенциал А', разумеется, равен нулю.

Теперь без особых хитростей можно найти потенциалы φ и Ав неподвижной системе координат. Соотношениями, обратными к уравнениям (25.24), будут

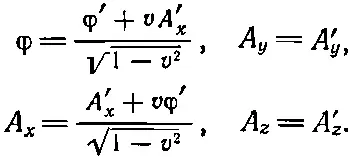(25.26)

Используя далее выражение для φ'[см. (25.25)] и равенство А'=0, получаем

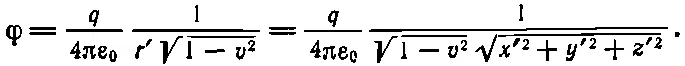
Эта формула дает нам скалярный потенциал φ, который мы увидели бы в системе S , но он, к сожалению, записан через координаты штрихованной системы. Впрочем, это дело легко поправимо; с помощью (25.1) можно выразить t ', х ', у ', z ' через t, x, у, z и получить

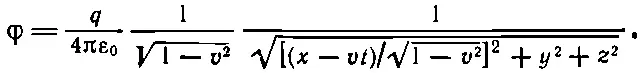(25.27)

Повторяя ту же процедуру для вектора А, вы можете показать, что

(25.28)

Это те же самые формулы, которые мы вывели в гл. 21, но там они были получены другим методом.

Итак, потенциалы φ и А, оказывается, образуют в совокупности четырехвектор, который мы обозначили через А μ, а волновое уравнение (полное уравнение, выражающее А μчерез j μ) можно записать в виде (25.22). Это уравнение вместе с сохранением заряда (25.19) составляют фундаментальный закон электромагнитного поля:

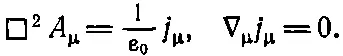(25.29)

И вот, пожалуйста, все уравнения Максвелла просто и красиво записываются всего в одной строке. Достигли ли мы чего-нибудь, записав их в таком виде, кроме, разумеется, красоты и простоты? Прежде всего, есть ли здесь какое-нибудь отличие от того, что было раньше, когда мы выписывали их во всем разнообразии компонент? Можно ли из этих уравнений получить нечто, чего нельзя получить из волновых уравнений для потенциалов, содержащих заряды и токи? Ответ вполне определенный — конечно, нельзя. Единственное, что мы сделали — это изменили названия, т. е. использовали новые обозначения. Мы нарисовали квадратик для обозначения производных, но это по-прежнему не более и не менее как вторая производная по t минус вторая производная по х , минус вторая производная по у , минус вторая производная по z. А значок μ, говорит, что у нас есть четыре уравнения, по одному для каждого из значений μ= t, х, у или z. Какой же тогда смысл того, что уравнения можно записать в столь простой форме? С точки зрения получения чего-то нового — никакого. Хотя, возможно, простота уравнений и выражает определенную простоту природы. Сейчас я покажу вам нечто интересное, чему мы понемногу научились. Можно сказать, что все законы физики описываются одним уравнением :