Ричард Фейнман - Том 2. Электромагнетизм и материя

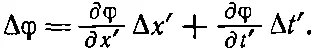
Используя уравнение (25.1), мы можем выразить Δ х ' и Δ t ' через Δ t . Вспоминая теперь, что величина х постоянна, так что Δx=0, мы пишем

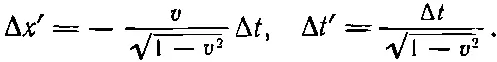
Таким образом,

Сравнивая этот результат с (25.13), мы узнаем, что

(25.14)

Аналогичные вычисления дают

(25.15)

Теперь вы видите, что градиент получился довольно странным. Выражения для х и t через х ' и t ' [полученные решением уравнений (25.1)] имеют вид

Именно так должен преобразовываться четырехвектор. Но в уравнениях (25.14) и (25.15) знаки получились неправильными! Выход в том, что надо заменить неправильное определение четырехмерного оператора градиента (∂/∂ t ,∇) правильным:

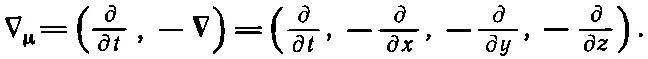(25.16)

Мы его обозначим ∇ μ. Для такого ∇ μтрудности исчезают, и он ведет себя так, как подобает настоящему четырехвектору. (Ужасно неприятно наличие минусов, но так уж устроено в мире.) Разумеется, говоря, что ∇ μ«ведет себя как четырехвектор», мы подразумеваем, что четырехмерный градиент скалярной функции есть четырехвектор. Если φ — настоящее скалярное (лоренц-инвариантное) поле, то ∇ μφ будет четырехвекторным полем.

Итак, все уладилось. Теперь у нас есть векторы, градиенты и скалярное произведение. Следующий на очереди — инвариант, аналогичный дивергенции в трехмерном векторном анализе. Ясно, что аналогом его должно быть выражение ∇ μb μ, где b μ— векторное поле, компоненты которого являются функциями пространства и времени. Мы определим дивергенцию четырехвектора b μ=( b t , b) как скалярное произведение ∇ μна b μ:

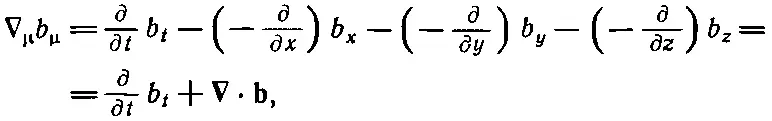(25.17)

где ∇·b— обычная трехмерная дивергенция вектора b. Не забывайте внимательно следить за знаками. Один знак минус связан с определением скалярного произведения [формула (25.7)], а другой возникает от пространственных компонент ∇ μ[формула (25.16)]. Дивергенция, определяемая формулой (25.7), есть инвариант, и для всех систем координат, отличающихся друг от друга преобразованием Лоренца, применение ее приводит к одинаковой величине.

Остановимся теперь на физическом примере, в котором появляется четырехмерная дивергенция. Ею можно воспользоваться при решении задачи о полях вокруг движущегося проводника. Мы уже видели (гл. 13, § 7, вып. 5), что плотность электрического заряда ρ и плотность тока j образуют четырехвектор j μ=( p, j ). Если незаряженный провод переносит ток j x , то в системе отсчета, движущейся относительно него со скоростью v (вдоль оси х ), в проводнике наряду с током появится и заряд [который возникает согласно закону преобразований Лоренца (25.1)]:

Но это как раз то, что мы нашли в гл. 13. Теперь нужно подставить эти источники в уравнение Максвелла в движущейся системе и найти поля.

Закон сохранения заряда в четырехмерных обозначениях тоже принимает очень простой вид. Рассмотрим четырехмерную дивергенцию вектора j μ:

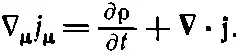(25.18)

Закон сохранения заряда утверждает, что утекание тока из единицы объема должно быть равно отрицательной скорости увеличения плотности заряда. Иными словами,

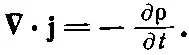
Подставляя это в (25.18), получаем очень простую форму закона сохранения заряда:

(25.19)

Благодаря тому что ∇ μj μ— инвариант, равенство его нулю в одной системе отсчета означает равенство нулю и во всех других. Таким образом, если заряд сохраняется в одной системе, он будет сохраняться и во всех других системах координат, движущихся относительно нее с постоянной скоростью.

В качестве последнего примера рассмотрим скалярное произведение оператора градиента ∇ μна себя. В трехмерном пространстве такое произведение дает лапласиан

Что получится для четырех измерений? Вычислить это очень просто. Следуя нашему правилу скалярного произведения, находим

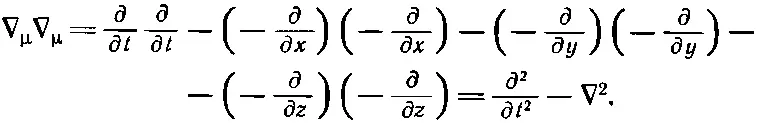
Этот оператор, представляющий аналог трехмерного лапласиана, называется даламбертианом и обозначается специальным символом

(25.20)

По построению он является скалярным оператором, т. е., если подействовать им, скажем, на четырехвекторное поле, возникает новое четырехвекторное поле. [Иногда даламбертиан определяется с противоположным по отношению к (25.20) знаком, так что при чтении литературы будьте внимательны!]

Итак, для большинства величин, перечисленных нами в табл. 25.1, мы нашли их четырехмерные эквиваленты. (У нас еще нет эквивалента векторного произведения, но его нахождение мы оставим до следующей главы.) А теперь соберем в одно место все важнейшие результаты и определения и составим еще одну таблицу (табл. 25.2); она поможет вам лучше запомнить, что во что переходит.

В гл. 18, § 6, мы уже сталкивались с оператором Даламбера, хотя и не знали, что он так называется. Мы нашли там дифференциальное уравнение для потенциалов, которое в новых обозначениях выглядит так: