Ричард Фейнман - Том 2. Электромагнетизм и материя

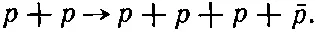
Иначе говоря, высокоэнергетический протон сталкивается с покоящимся протоном (например, с помещенной в пучок водородной мишенью), и если падающий протон обладает достаточной энергией, то вдобавок к двум первоначальным протонам может родиться пара протон—антипротон [32] Вас может удивить, почему же мы не пользуемся реакцией Или даже для которой, несомненно, требуется меньшая энергия? Все дело в принципе, называемом сохранением барионного заряда, согласно которому величина, равная числу протонов минус число антипротонов, не может измениться. В левой стороне нашей реакции эта величина равна 2. Следовательно, если мы хотим справа иметь антипротон, то ему должны сопутствовать еще три протона (или других бариона). .

Какой энергией должен обладать падающий протон, чтобы эта реакция стала энергетически возможной?

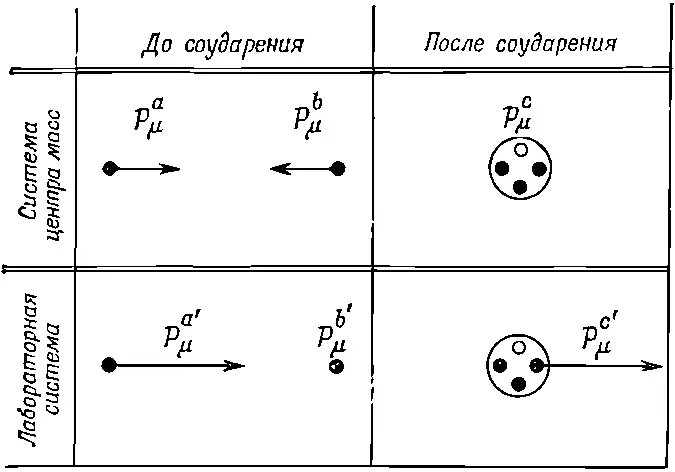
Фиг. 25.1. Реакция р+p → Зр+ — р в лабораторной системе и системе ц. м. Предполагается, что энергия падающего протона как раз достаточна для протекания реакции. Протоны обозначены черными кружочками, а антипротоны —белыми.

Ответ легче всего получить, рассмотрев эту реакцию в системе центра масс (ц. м.) (фиг. 25.1). Назовем падающий протон протоном а , а его четырехимпульс обозначим через р μ a . Аналогично, протон мишени назовем b, а его четырехимпульс обозначим через р μ b . Если энергии падающего протона как раз достаточно для реакции, то в конечном состоянии (т. е. в состоянии после соударения) образуется система, содержащая три протона и антипротон, покоящиеся в системе ц. м. Если энергия падающего протона будет несколько выше, то частицы в конечном состоянии вылетят с некоторой кинетической энергией и будут разлетаться в стороны; если же она немного ниже, то ее будет недостаточно для образования четырех частиц.

Пусть р μ с — полный четырехимпульс всей системы в конечном состоянии, тогда, согласно закону сохранения энергии и импульса,

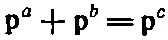
и

а комбинируя эти два выражения, можно написать

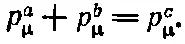(25.9)

Теперь еще одно важное обстоятельство: поскольку мы получили уравнение для четырехвекторов, то оно должно выполняться в любой инерциальной системе. Этим фактом можно воспользоваться для упрощения вычислений. Напишем длины каждой из частей (25.9), которые, разумеется, тоже должны быть равны друг другу, т. е.

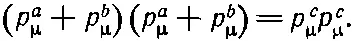(25.10)

Так как р μ с р μ с — инвариант, то можно вычислить его в какой-то одной системе координат. В системе ц. м. временная компонента р μ с равна энергии покоя четырех протонов, т. е. 4М, а пространственная часть р равна нулю, так что р μ с =(4М, 0). При этом мы воспользовались равенством масс протона и антипротона, обозначив их одной буквой М .

Таким образом, уравнение (25.10) принимает вид

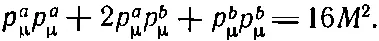(25.11)

Произведения р μ а р μ а и p μ b p μ b , вычисляются очень быстро: «длина» четырехвектора импульса любой частицы равна просто квадрату ее массы:

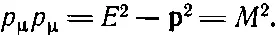
Это можно доказать прямыми вычислениями или, несколько более эффектно, простым замечанием, что в системе покоя частицы р μ=( М , 0), а следовательно, р μ р μ=М 2. А так как это инвариант, то он равен М 2в любой системе отсчета. Подставляя результаты в уравнение (25.11), мы получаем

или

(25.12)

Теперь можно вычислить р μ а р μ b в лабораторной системе. В этой системе четырехвектор р μ а =( Е а , р а ), а р μ b =( М , 0), ибо он описывает покоящийся протон. Итак, р μ а р μ b должно быть равно МЕ а , а мы знаем, что скалярное произведение — это инвариант, поэтому оно должно быть равно значению, найденному нами в (25.12). В результате получается

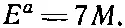
Полная энергия падающего протона должна быть по меньшей мере равна 7 М (что составляет около 6,6 Гэв , так как М=938 Мэв ) или после вычитания массы покоя М получаем, что кинетическая энергия должна быть равна по меньшей мере 6М (около 5,6 Гэв ). Именно с тем, чтобы иметь возможность производить антипротоны, бетатрон в Беркли проектировался на кинетическую энергию ускоренных протонов около 6.2 Гэв .

Скалярное произведение — инвариант, поэтому полезно знать его величину. Что, например, можно сказать о «длине» четырехвектора скорости u μu μ?

т. е. u μ— единичный четырехвектор .

Следующей величиной, которую нам следует обсудить, является четырехмерный аналог градиента. Напомним (см. гл. 14, вып. 1), что три оператора дифференцирования ∂/∂ x , ∂/∂ y , ∂/∂ z преобразуются подобно трехмерному вектору и называются градиентом. Та же схема должна работать и в четырех измерениях; по простоте вы можете подумать, что четырехмерным градиентом должны быть (∂/∂ t , ∂/∂ x , ∂/∂ y ∂/∂ z ), но это неверно .

Чтобы обнаружить ошибку, рассмотрим скалярную функцию, которая зависит только от х и t . Приращение φ при малом изменении t на Δt и постоянном х равно

(25.13)

С другой стороны, с точки зрения движущегося наблюдателя