Ричард Фейнман - Том 2. Электромагнетизм и материя

Рассечем наш волновод горизонтально, как показано на фиг. 24.15, где W 1и W 2— стенки волновода, а S 0— источник (провод).

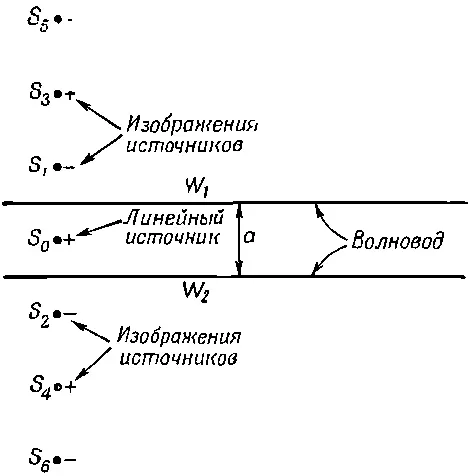
Фиг. 24.15. Линейный источник S 0 между проводящими плоскими стенками W 1 и W 2 . Стенки можно заменить бесконечной последовательностью изображений источников.

Обозначим направление тока в проводе знаком плюс. Будь у волновода лишь одна стенка, скажем W 1, ее можно было бы убрать, поместив изображение источника (с противоположной полярностью) в точке S 1. Но при двух стенках появится также изображение S 0в стенке W 2; обозначим его S 2. Этот источник также будет обладать своим изображением в W 1; обозначим его S 3. Дальше, сами S 1и S 3изобразятся в W 2точками S 4и S 6и т. д. И для нашей пары плоских проводников с источником посредине поле между проводниками совпадет с полем, генерируемым бесконечной цепочкой источников на расстоянии а друг от друга. (Это на самом деле как раз то, что вы увидите , посмотрев на провод, расположенный посредине между двумя параллельными зеркалами.) Чтобы поля обращались в нуль на стенках, полярности токов в изображениях должны меняться от одного изображения к следующему. Иначе говоря, их фаза меняется на 180°. Поле волновода — это просто суперпозиция полей всей этой бесконечной совокупности линейных источников.

Известно, что вблизи от источников поле очень напоминает статические поля. В гл. 7, § 5 (вып. 5) мы рассматривали статическое поле сетки линейных источников и нашли, что оно похоже на поле заряженной пластины, если не считать членов ряда, убывающих по мере удаления от сетки экспоненциально. У нас средняя сила источников равна нулю, потому что у каждой пары соседних источников знаки противоположны. Любые поля, существующие здесь, должны с расстоянием убывать экспоненциально. Вплотную к источнику мы в основном воспринимаем поле этого ближайшего источника; на больших расстояниях уже воздействует несколько источников, и их суммарное влияние дает нуль. Мы теперь понимаем, отчего волновод ниже граничной частоты дает экспоненциально убывающее поле. При низких частотах годится статическое приближение, и оно предсказывает быстрое ослабление полей с расстоянием.

Теперь зато возникает противоположный вопрос: отчего же в таком случае волны вообще распространяются? Теперь уже это выглядит таинственно! А причина-то в том, что при высоких частотах запаздывание полей может внести в фазу добавочные изменения, которые могут привести к тому, что поля источников с противоположной фазой будут усиливать, а не гасить друг друга. В гл. 29 (вып. 3) мы уже изучали как раз для этой задачи поля, создаваемые системой антенн или оптической решеткой. Тогда мы обнаружили, что соответствующее расположение нескольких радиоантенн может привести к такой интерференционной картине, что в одном направлении сигнал будет очень сильный, а в других сигналов вообще не будет.

Вернемся к фиг. 24.15 и посмотрим на поля на большом расстоянии от линии изображений источников. Поля будут велики лишь в некоторых направлениях, зависящих от частоты, именно в тех направлениях, в каких поля всех источников попадают в фазу друг к другу и складываются. На заметном расстоянии от источников поле в этих специальных направлениях распространяется как плоские волны. Мы изобразили такую волну на фиг. 24.16, где сплошными линиями даны гребни волн, а штрихом — впадины.

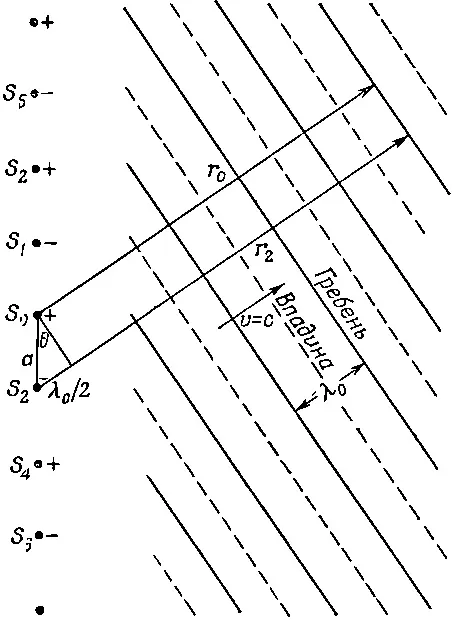
Фиг. 24.16. Одна совокупность когерентных волн от вереницы линейных источников.

Направление волны должно быть таким, чтобы разность запаздываний от двух соседних источников до гребня волны отвечала полупериоду колебания. Иными словами, разность между r 2и r 0на рисунке равна половине длины волны в пустом пространстве:

Тогда угол θ дается условием

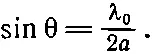(24.33)

Имеется, конечно, и другая совокупность волн, бегущих вниз под симметричным углом по отношению к линии источников. А полное поле в волноводе (не слишком близко к источнику) является суперпозицией этих двух совокупностей волн (фиг. 24.17).

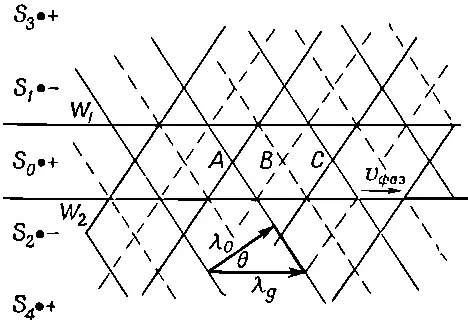
Фиг. 24.17. Поле в волноводе можно рассматривать как наложение двух верениц плоских волн.

Конечно, в действительности картина истинных полей совпадает с изображенной лишь в пространстве между стенками волновода.

В таких точках, как А и С , гребни двух волновых картин совпадут, и у поля будет максимум; в точках же наподобие В пики обеих волн направлены в отрицательную сторону, и поле обладает минимумом (наименьшим отрицательным значением). С течением времени поле в волноводе будет двигаться вдоль него. Длина волны будет равна λ g — расстоянию от A до С . Она связана с θ формулой

(24.34)

Подставляя (24.33) вместо θ, получаем

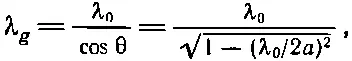(24.35)

что в точности совпадает с (24.19).

Теперь нам становится понятно, почему волны распространяются только выше граничной частоты ω 0. Если длина волн в пустом пространстве больше 2 а , то не существует угла, под которым может появиться волна, показанная на фиг. 24.16. Необходимая для этого конструктивная интерференция возникает внезапно, едва λ 0оказывается меньше 2 а , или, что то же самое, когда ω 0=πс/а.

А если частота достаточно высока, то может появиться два или больше возможных направления распространения волн. В нашем случае это произойдет при λ 0< 2/ 3 а . Но вообще-то это может происходить и при λ 0<���а. Эти добавочные волны отвечают высшим типам волн, о которых мы говорили.

После нашего анализа становится также ясно, отчего фазовая скорость волн, бегущих по трубе, превышает с и зависит от ω. Когда ω меняется, меняется и угол на фиг. 24.16, под которым в пустом пространстве распространяются волны, а вместе с этим меняется и скорость вдоль трубы.

Хотя мы описали волны в волноводе в виде суперпозиции полей бесконечной совокупности линейных источников, но можно убедиться в том, что тот же результат можно было бы получить, представив себе две совокупности волн в пустом пространстве, многократно отражаемых от двух идеальных зеркал вперед и назад, и вспоминая, что подобное отражение означает перемену знака фазы. Эти совокупности отражаемых волн гасили бы друг друга под всеми углами, кроме угла θ [см. (24.33)]. Одну и ту же вещь можно рассматривать многими способами.