Ричард Фейнман - Том 2. Электромагнетизм и материя

Самое интересное то, что единого способа избавиться от неопределенности энергии поля, по-видимому, вообще нет. Иногда утверждают, что эту проблему можно разрешить, используя теорию гравитации; при этом приводятся такие доводы. В теории гравитации источником гравитационного притяжения является вся энергия. Поэтому если нам известно, какие гравитационные силы действуют на свет, то можно правильно определить плотность энергии электричества. До сих пор, однако, такими тонкими экспериментами, которые позволили бы точно определить гравитационное влияние на электромагнитное поле, никто не занимался. Впрочем, установлено, что свет при прохождении около Солнца отклоняется, поэтому мы можем говорить, что Солнце притягивает к себе свет. Во всяком случае, найденные нами выражения для электромагнитной энергии и потока всегда всеми признавались. И хотя иногда результаты, полученные с их использованием, казались странными, никто никогда не обнаружил в них чего-то невероятного, какого-то расхождения с экспериментом. Согласимся со всеми и будем считать, что, по-видимому, здесь все в порядке.

Мне хотелось бы сделать еще одно замечание о формуле для энергий. Прежде всего формула для энергии поля в единице объема очень проста — это сумма электрической и магнитной энергий, если электрическую энергию мы определим как Е 2, а магнитную — как В 2. Эти выражения были найдены нами как возможные выражения для энергии при рассмотрении статических задач. Кроме него, мы нашли для энергии электростатического поля и несколько других выражений, например ρφ, которое в электростатическом случае равно интегралу от Е·Е. Однако в электродинамическом случае это равенство нарушается, и нет критерия, позволяющего установить, которая из формул правильна. Но теперь мы это знаем. Аналогично, мы нашли выражение для магнитной энергии, которое верно в самом общем случае.

Наша формула для вектора потока энергии Sпредставляет нечто новое. Теперь следует посмотреть, насколько она годится в некоторых специальных случаях, а также проверить ее на том, что мы знали раньше. Первым нашим примером будет свет. В световой волне векторы Еи Внаправлены под прямым углом друг к другу и направлению распространения волны (фиг. 27.2).

Фиг. 27.2. Векторы Е, В и S световой волны.

В электромагнитной волне величина В равна (1/с) Е , а поскольку они направлены под прямым углом, то величина ( Е× B) равна просто Е 2/ с . Таким образом, для света поток энергии в секунду через единичную поверхность равен

(27.16)

В световой волне, где E = E 0 cos ω( t - х / с ), средняя скорость потока энергии через единичную площадь ср, которая называется «интенсивностью» света, равна среднему значению электрического поля, помноженному на ε 0 с :

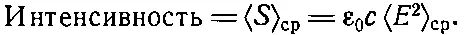(27.17)

Этот результат, как ни странно, мы уже получали в гл. 31, § 5 (вып. 3), когда изучали свет. Мы получили его совсем другим путем и поэтому можем сейчас в него поверить. Когда у нас есть пучок света, то плотность энергии в пространстве задается уравнением (27.14). Воспользовавшись теперь тем, что в световой волне сВ = Е , получаем

Однако вектор Еизменяется в пространстве, поэтому средняя плотность энергии равна

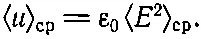(27.18)

Далее, свет распространяется со скоростью с, поэтому можно думать, что энергия, проходящая в секунду через квадратный метр, равна произведению с на количество энергии в кубическом метре, т. е.

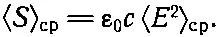
Все в порядке. Мы снова получили выражение (27.17).

Возьмем теперь другой пример, на этот раз очень любопытный. Рассмотрим поток энергии в медленно заряжающемся конденсаторе. (Мы не хотим сейчас иметь дело со столь высокими частотами, при которых конденсатор становится похожим на резонансную полость, но нам не нужен и постоянный ток.) Возьмем обычный конденсатор с круглыми параллельными пластинами (фиг. 27.3). Между ними создается почти однородное электрическое поле, которое изменяется с течением времени. Полная электромагнитная энергия внутри конденсатора в любой момент равна произведению плотности энергии и на объем. Если радиус пластин равен а , а расстояние между ними h , то полная энергия, заключенная между пластинами, будет

(27.19)

С изменением напряженности Е эта энергия тоже меняется. Когда конденсатор заряжается, внутренний объем приобретает энергию со скоростью

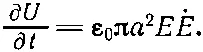(27.20)

Так что должен существовать поток энергии, направленный откуда-то со стороны внутрь объема. Вы, конечно, думаете, что он идет от проводов, заряжающих конденсатор,— а вот и нет! Поток внутрь никоим образом не может идти с этой стороны, так как Еперпендикулярно к пластинам, а поэтому Е× Bдолжно быть параллельно им.

Вы, вероятно, помните, что при зарядке конденсатора возникает магнитное поле, которое направлено по окружности вокруг оси. Об этом говорилось в гл. 23. Воспользовавшись последним уравнением Максвелла, мы там нашли, что магнитное поле на краю конденсатора определяется выражением

или

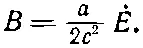
Направление его показано на фиг. 27.3.

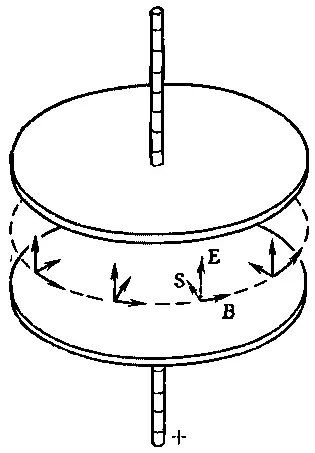
Фиг. 27.3. Вблизи заряженного конденсатора вектор Пойнтинга S направлен внутрь него