Ричард Фейнман - Том 2. Электромагнетизм и материя

Я расскажу вам еще об одной теории, чтобы показать, до каких вещей додумываются люди, когда они увлечены. Это несколько другая модификация законов электродинамики, которую предложил Бопп.

Вы понимаете, что, решившись изменить уравнения электромагнетизма, можно делать это в любом месте. Вы можете изменить закон сил, действующих на электрон, или можете изменить уравнения Максвелла (как это будет сделано в теории, которую я собираюсь описать) или еще что-нибудь. Одна из возможностей — изменить формулы, определяющие потенциал через заряды и токи. Возьмем формулу, которая выражает потенциалы в некоторой точке через плотности токов (или зарядов) в любой другой точке в ранний момент времени. С помощью четырехвекторных обозначений для потенциалов мы можем записать ее в виде

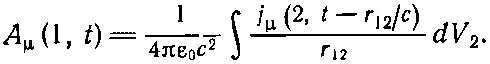(28.13)

Удивительно простая идея Боппа заключается в следующем. Может быть, все зло происходит от множителя 1/r под интегралом. Предположим с самого начала, что потенциал в одной точке зависит от плотности зарядов в любой точке как некоторая функция расстояния между точками, скажем как f(r 12). Тогда полный потенциал в точке 1 будет определяться интегралом по всему пространству от произведения j μна эту функцию

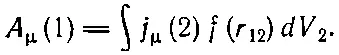
Вот и все. Никаких дифференциальных уравнений, ничего больше. Есть только еще одно условие. Мы должны потребовать, чтобы результат был релятивистски инвариантным. Так что в качестве «расстояния» мы должны взять инвариантное «расстояние» между двумя точками в пространстве-времени. Квадрат этого расстояния (с точностью до знака, который несуществен) равен

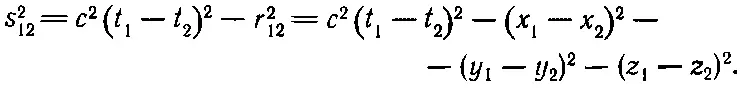(28.14)

Так что для релятивистской инвариантности теории функция должна зависеть от s 12или, что то же самое, от s 12 2. Таким образом, в теории Боппа

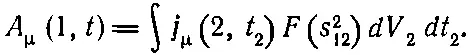(28.15)

(Интеграл, разумеется, должен браться по четырехмерному объему dt 2 dx 2 dy 2 dz 2.)

Теперь остается только выбрать подходящую функцию F . Относительно нее мы предполагаем только одно, что она повсюду мала, за исключением области аргумента вблизи нуля, т. е. что график F ведет себя подобно кривой, изображенной на фиг. 28.4.

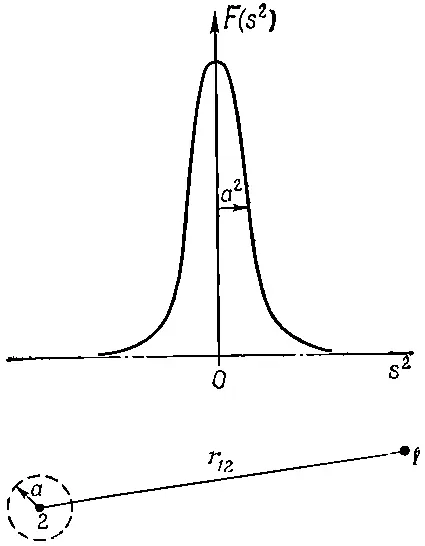
Фиг. 28,4. Функция F(s 2 ), используемая в нелокальной теории Боппа.

Это узкий пик в окрестности s 2=0, шириной которого грубо можно считать величину а 2. Если вычисляется потенциал в точке 1, то приближенно можно утверждать, что заметный вклад дают только те точки 2, для которых s 12 2=с 2(t 2-t 1) 2-r 12 2отличается от нуля на ±a 2. Это можно выразить, сказав, что F важно только для

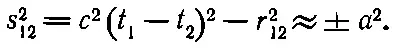(28.16)

Если понадобится, можно проделать все математически более строго, но идея вам уже ясна.

Предположим теперь, что а очень мало по сравнению с размерами обычных объектов типа электромоторов, генераторов и тому подобное, поэтому для обычных задач г 12≫а. Тогда выражение (28.16) говорит, что в интеграл (28.15) дают вклад только те токи, для которых t 1-t 2очень мало:

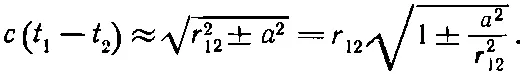
Но поскольку а 2/r 12 2≪1, то квадратный корень приближенно равен 1 ±а 2/2r 12 2, так что

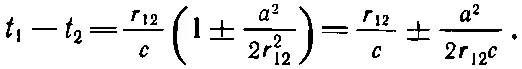
В чем здесь суть? Полученный результат говорит, что для А μв момент t 1важны только те времена t 2, которые отличаются от него на запаздывание r 12/c с пренебрежимо малой поправкой, ибо r 12≫а. Другими словами, теория Боппа переходит в теорию Максвелла при удалении от зарядов в том смысле, что она приводит к эффекту запаздывания.

Мы можем приближенно увидеть, к чему нас приведет интеграл (28.15). Если, зафиксировав r 12, провести интегрирование по t 2в пределах от -∞ до +∞,то s 12 2тоже будет изменяться от -∞ до +∞. Но основной вклад даст участок по t 2шириной Δt 2=2·а 2/2r 12с с центром в момент t 1-r 12/c. Пусть функция F (s 2) при s 2=0 принимает значение К , тогда интегрирование по t 2дает приблизительно Kj μΔt 2, или

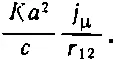
Разумеется, величину j μследует взять в момент t 2=t 1-r 12/c, так что (28.15) принимает вид

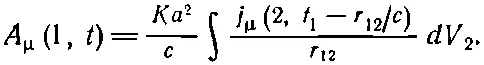
Если выбрать K=q 2с/4πε 0а 2, то мы придем прямо к запаздывающему решению уравнений Максвелла для потенциалов, причем автоматически возникает зависимость 1/r! И все это получилось из простого предположения, что потенциал в одной точке пространства-времени зависит от плотности токов во всех других точках пространства-времени с весовым множителем, в качестве которого взята некая функция четырехмерного расстояния между двумя точками. Эта теория тоже дает конечную электромагнитную массу электрона, а соотношение между энергией и массой как раз такое, какое требуется в теории относительности. Ничего другого не могло и быть, ибо теория релятивистски инвариантна с самого начала.

Однако и этой теории и всем другим описанным нами теориям можно предъявить тяжкое обвинение. Все известные нам частицы подчиняются законам квантовой механики, поэтому необходима квантовомеханическая форма электродинамики. Свет ведет себя подобно фотонам. Это уже не 100-процентная теория Максвелла. Следовательно, электродинамика должна быть изменена. Мы уже говорили, что упорное старание исправить классическую теорию может оказаться напрасной тратой времени, ибо в квантовой электродинамике трудности могут исчезнуть или будут разрешены другим образом. Однако и в квантовой электродинамике трудности не исчезают. В этом кроется одна из причин, почему люди потратили столько времени, пытаясь преодолеть классические трудности и надеясь, что если они смогут преодолеть их, то после квантового обобщения уравнений Максвелла все будет в порядке. Однако и после такого обобщения трудности не исчезают.