Ричард Фейнман - Том 2. Электромагнетизм и материя

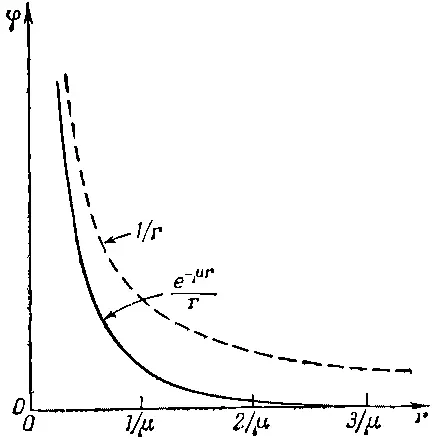
Фиг. 28.6. Сравнение потенциала Юкавы. е -μr/r с кулоновым потенциалом 1/r.

Поэтому «радиус действия» ядерных сил гораздо меньше «радиуса действия» электростатических. Экспериментально доказано, что ядерные силы не простираются на расстояния свыше 10 -13 см , поэтому μ≈10 15 м -1.

И, наконец, давайте рассмотрим волновое решение уравнения (28.17). Если мы подставим в него

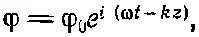
то получим

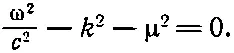
Связывая теперь частоту с энергией, а волновое число с импульсом, как это делалось в конце гл. 34 (вып. 3), мы найдем соотношение

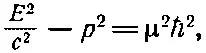
которое говорит, что масса «фотона» Юкавы равна μℏ/ с . Если в качестве μ взять величину ~10 15м -1, которую дает наблюдаемый радиус действия ядерных сил, то масса оказывается равной 3·10 -25г, или 170 Мэв, что приблизительно равно наблюдаемой массе π-мезона. Таким образом, по аналогии с электродинамикой мы бы сказали, что π-мезон — это «фотон» поля ядерных сил. Однако теперь мы распространили идеи электродинамики в такую область, где они на самом деле могут оказаться и неверными. Мы вышли далеко за рамки электродинамики и очутились перед проблемой ядерных сил.

Повторить : гл. 30 (вып. 3) «Дифракция».

Мы теперь перейдем к описанию в общих чертах движения зарядов в различных условиях. Наиболее интересные явления возникают тогда, когда зарядов движется много и все они взаимодействуют друг с другом. Так обстоит дело, когда электромагнитные волны проходят через кусок вещества или плазму; тогда легионы зарядов взаимодействуют друг с другом. Но это очень сложная картина. Позднее мы поговорим и о таких проблемах; пока же мы обсудим несравненно более простую задачу о движении отдельного заряда в заданном поле. При этом можно пренебречь всеми другими зарядами, за исключением, разумеется, тех зарядов и токов, которые создают предполагаемое нами поле.

Начать, по-видимому, нужно с движения частицы в однородном электрическом поле. Движение при небольших скоростях не представляет особенного интереса — это просто равномерно ускоренное движение в направлении поля. А вот когда частица, набрав достаточно энергии, превращается в релятивистскую, движение ее становится более сложным. Решение для этого случая я оставляю вам — потрудитесь и отыщите его сами.

Мы же рассмотрим движение в однородном магнитном поле, когда электрического поля нет. Эту задачу мы уже решали. Одним из решений было движение частиц по окружности. Магнитная сила q v× Ввсегда действует под прямым углом к направлению движения, так что производная d p/ dt перпендикулярна ри равна по величине vp / R , где R — радиус окружности, т. е.

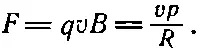
Таким образом, радиус круговой орбиты равен

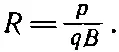(29.1)

Это одно из возможных движений. Если движущаяся частица имеет только одну составляющую в направлении поля, то она не изменяется, ибо у магнитной силы отсутствует компонента в направлении поля. Общее же движение частицы в однородном магнитном поле — это движение с постоянной скоростью в направлении Ви круговое движение под прямым углом к В, т. е. движение по цилиндрической спирали (фиг. 29.1).

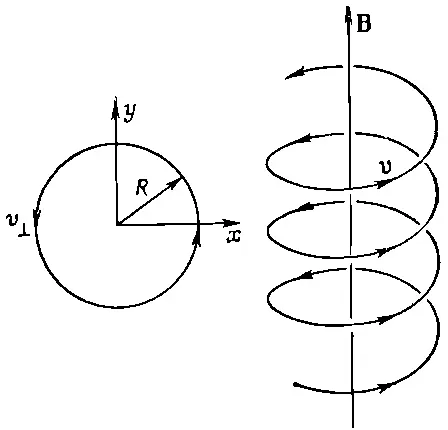
Фиг. 29.1. Движение частицы в однородном магнитном поле.

Радиус спирали определяется равенством (29.1) с заменой р на р ┴— компоненту импульса, перпендикулярную к направлению поля.

Однородное магнитное поле часто применяется в «анализаторе», или «спектрометре импульсов» высокоэнергетических частиц. Предположим, что в точке А (фиг. 29.2, а ) в однородное магнитное поле влетают заряженные частицы, причем магнитное поле перпендикулярно плоскости рисунка.

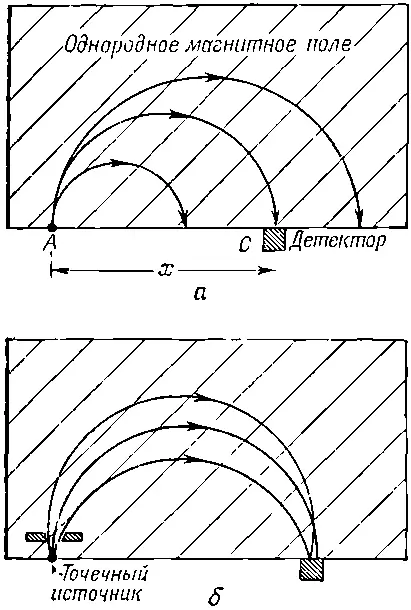
Фиг. 29.2. 180-градусный спектрометр импульсов с однородным магнитным полем. а — траектории частиц с разными импульсами; 6 — траектории частиц, влетающих под равными углами. Магнитное поле направлено перпендикулярно плоскости рисунка.

При этом каждая частица будет лететь по круговой орбите, радиус которой пропорционален ее импульсу. Если все частицы влетают в поле перпендикулярно его краю, то они покидают его на расстоянии х от точки А , пропорциональном их импульсу р . Помещенный в некоторой точке С счетчик будет регистрировать только такие частицы, импульс которых находится где-то в интервале Δр величин p = qBx /2.

Нет необходимости, разумеется, чтобы перед регистрацией частица поворачивалась на 180°, но такой «180-градусный спектрометр» обладает особым свойством: для него совсем необязательно, чтобы частицы входили под прямым углом к краю поля. На фиг. 29.2, б показаны траектории трех частиц с одинаковым импульсом, но входящих в поле под различными углами. Вы видите, что траектории у них разные, но все они покидают поле очень близко к точке С . В подобных случаях мы говорим о «фокусировке». Преимущество такого способа фокусировки в том, что она позволяет допускать в точку А частицы, летящие под большими углами, хотя обычно, как видно из рисунка, углы эти в какой-то степени ограничены. Большое угловое разрешение обычно означает регистрацию за данный промежуток времени большего числа частиц и сокращения, следовательно, времени измерения.

Изменяя магнитное поле, передвигая счетчик вдоль оси х или же покрывая с помощью многих счетчиков целую область по оси х , можно измерить «спектр» падающего пучка [«спектр» импульсов f ( p ) означает, что число частиц с импульсами в интервале между р и ( p + dp ) равно f(p)dp]. Такие измерения проводятся, например, при определении распределения по энергиям в β-распаде различных ядер.