Ричард Фейнман - Том 2. Электромагнетизм и материя

Имеется еще много других типов импульсных спектрометров, но я расскажу вам только об одном из них, характерном особенно большим разрешением по пространственному углу. В основе его лежат винтовые орбиты в однородном поле, как это показано на фиг. 29.1. Представьте себе цилиндрическую систему координат ρ, θ, z, причем ось z выбрана по направлению магнитного поля. Если частица испускается из начала координат под углом α к направлению оси z, то она будет двигаться по спиральной линии, описываемой выражением

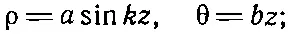
входящие туда параметры а, b и k нетрудно выразить через ρ, α и магнитное поле В . Если для данного импульса, но разных начальных углов отложить расстояние ρ от оси как функцию z , то мы получим кривые, подобные сплошным кривым на фиг. 29.3. (Вы помните — ведь это своего рода проекция винтовой траектории.)

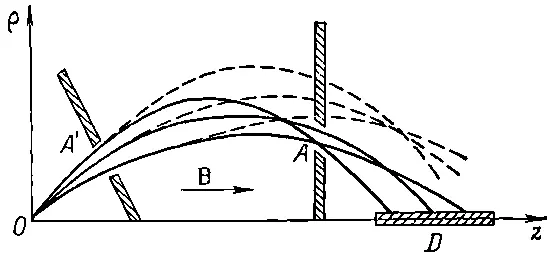
Фиг. 29.3. Спектрометр с аксиальным полем.

Когда угол между осью и начальным направлением велик, максимальное значение ρ тоже будет большим, а продольная скорость при этом уменьшается, так что выходящие под различными углами траектории стремятся собраться в своего рода фокус (точка А на рисунке). Если на расстоянии А поставить узкое кольцевое отверстие, то частицы, летящие в некоторой области углов, могут пройти через отверстие и достигнуть оси, где для их регистрации мы приготовим протяженный детектор D . Частицы, вылетающие из начала координат под тем же самым углом, но с большим импульсом, летят по пути, обозначенному нами пунктирной линией, и не могут пройти через отверстие А . Итак, прибор выбирает небольшой интервал импульса. Преимущество такого спектрометра по сравнению с описанным ранее состоит в том, что отверстия А и А ' можно сделать кольцевыми, так что могут быть зарегистрированы частицы в довольно большом телесном угле. Это преимущество особенно важно для слабых источников и при очень точных измерениях, когда необходимо использовать возможно большую долю испущенных источником частиц.

Но за это преимущество приходится расплачиваться, ибо метод требует большого объема однородного магнитного поля, и он практически пригоден только для частиц с небольшой энергией. Если вы помните, один из способов получения однородного поля — это намотать провод на сферу так, чтобы поверхностная плотность тока была пропорциональна синусу угла. Вы можете доказать, что то же самое справедливо и для эллипсоида вращения. Поэтому очень часто такой спектрометр изготовляют, просто наматывая эллипсоидальные витки на деревянный или алюминиевый каркас. Единственное, что при этом требуется,— это чтобы ток на любом интервале оси Δ х (фиг. 29.4) был одним и тем же.

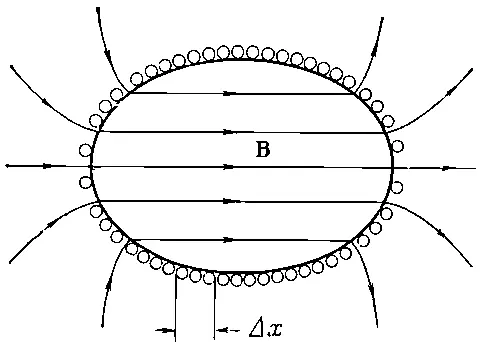
Фиг. 29.4. Внутри эллипсоидальной катушки, ток которой на любом интервале оси Δx одинаков, возникает однородное поле.

Фокусировка частицы имеет множество применений. Например, в телевизионной трубке электроны, вылетающие из катода, фокусируются на экране в маленькое пятнышко. Делается это для того, чтобы отобрать электроны одинаковой энергии, но летящие под различными углами, и собрать их в небольшую точку. Эта задача напоминает фокусировку света с помощью линз, поэтому устройства, которые выполняют такие функции, тоже называются линзами.

В качестве примера электронной линзы здесь приведена фиг. 29.5.

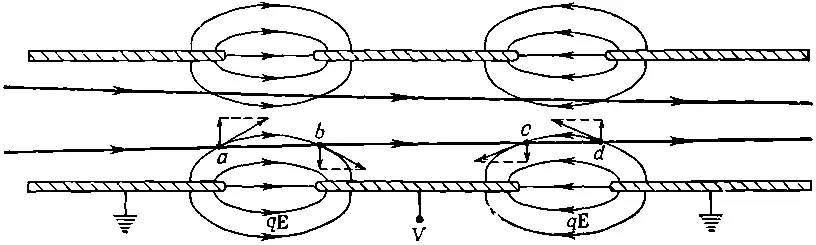
Фиг. 29.5. Электростатическая линза. Показаны силовые линии, т. е. линии вектора qE.

Это «электростатическая» линза, действие которой зависит от электрического поля между двумя соседними электродами. Работу ее можно понять, проследив за тем, что она делает со входящим слева параллельным пучком частиц. Попав в область а, электроны испытывают действие силы с боковой компонентой, которая прижимает их к оси. В области b электроны, казалось бы, должны получить равный по величине, но противоположный по знаку импульс, однако это не так. К тому времени, когда они достигнут области b , энергия их несколько увеличится, и поэтому на прохождение области b они затратят меньше времени . Силы-то те же самые, но время их действия меньше, поэтому и импульс будет меньше. А полный импульс силы при прохождении областей а и b направлен к оси, так что в результате электроны стягиваются к одной общей точке. Покидая область высокого напряжения, частицы получают добавочный толчок по направлению к оси. В области с сила направлена от оси, а в области d — к оси, но во второй области частица остается дольше, так что снова полный импульс направлен к оси. Для небольших расстояний от оси полный импульс силы на протяжении всей линзы пропорционален расстоянию от оси (понимаете почему?), и это как раз основное условие, необходимое для обеспечения фокусировки линз такого типа.

С помощью этих же рассуждений вы можете убедиться, что фокусировка будет достигнута во всех случаях, когда потенциал в середине электрода по отношению к двум другим либо положителен, либо отрицателен. Электростатические линзы такого типа обычно используются в катоднолучевых трубках и некоторых электронных микроскопах.

Есть еще один сорт линз — их часто можно встретить в электронных микроскопах — это магнитные линзы. Схематически они изображены на фиг. 29.6.

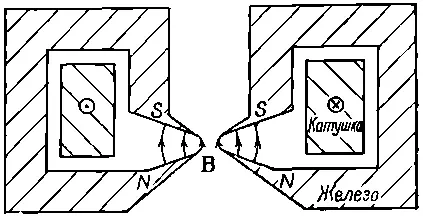
Фиг. 29.6. Магнитная линза.

Цилиндрически симметричный электромагнит с очень острыми кольцевыми наконечниками полюсов создает в малой области очень сильное неоднородное магнитное поле. Оно фокусирует электроны, летящие вертикально через эту область. Механизм фокусировки нетрудно понять; посмотрите увеличенное изображение области вблизи наконечников полюсов на фиг. 29.7.

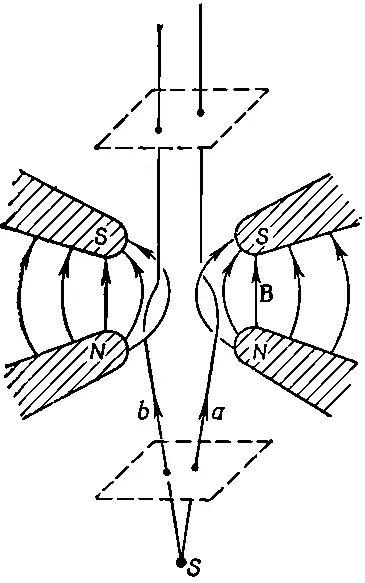
Фиг. 29.7. Движение электрона в магнитной линзе.