Ричард Фейнман - Том 2. Электромагнетизм и материя

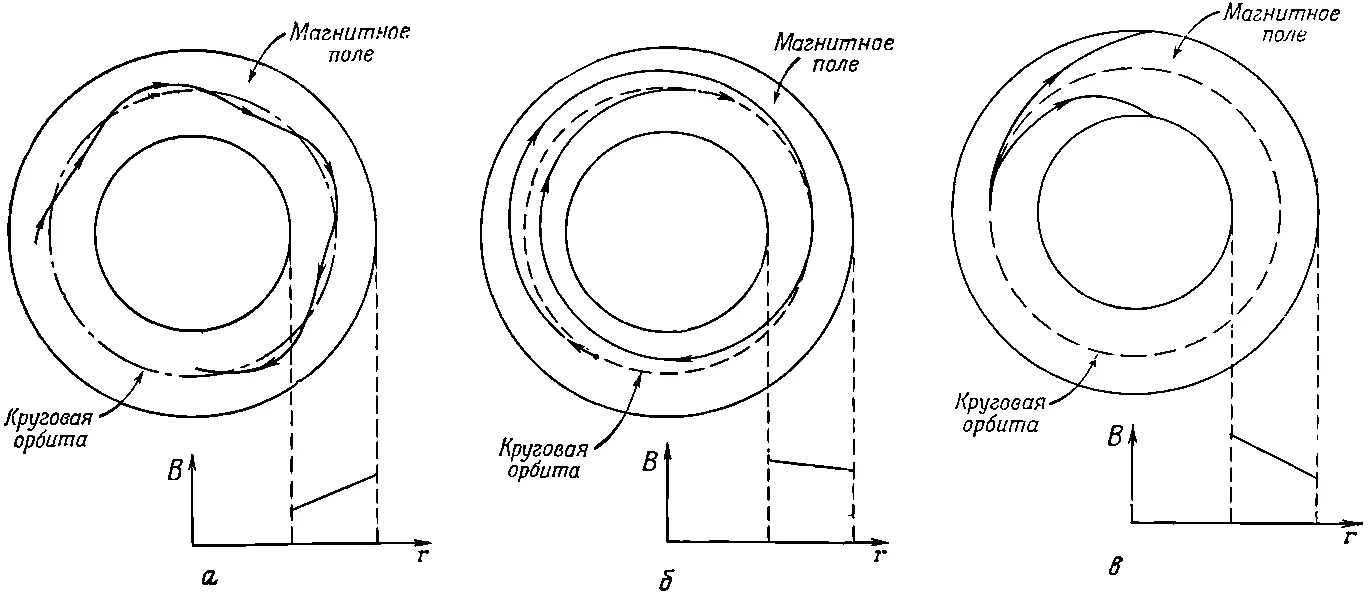
Фиг. 29.11. Радиальное движение частицы в магнитном поле. а — с большим положительным «наклоном»; б — с малым отрицательным «наклоном»; в — с большим отрицательным «наклоном».

Фактически радиальная фокусировка происходит даже при противоположном «наклоне». Это может происходить в тех случаях, когда радиус кривизны траектории увеличивается не быстрее, чем расстояние частицы от центра поля. Орбиты частиц будут подобны изображенным на фиг. 29.11,б. Но если градиент поля слишком велик, то частицы не вернутся на желаемый радиус, а будут по спирали выходить из поля либо внутрь, либо наружу (фиг. 29.11, в ).

«Наклон» поля мы обычно характеризуем «относительным градиентом», или индексом поля n

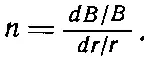(29.2)

Направляющее поле создает радиальную фокусировку, если относительный градиент будет больше -1.

Радиальный градиент поля приведет также к вертикальным силам, действующим на частицу. Предположим, мы имеем поле, которое вблизи центра орбиты сильнее, а снаружи слабее. Вертикальное поперечное сечение магнита под прямым углом к орбите может иметь такой вид, как показано на фиг. 29.12. (Причем протоны летят на нас из страницы.)

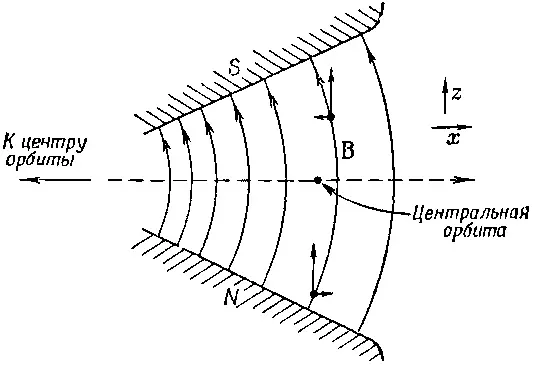
Фиг. 29.12. Вертикально фокусирующее поле. Вид в поперечном сечении, перпендикулярном к орбите.

Если нам нужно, чтобы поле было сильнее слева и слабее справа, то магнитные силовые линии должны быть искривлены подобно изображенным на рисунке. То, что это должно быть так, можно увидеть из закона равенства нулю циркуляции Вв пустом пространстве. Если выбрать систему координат, показанную на рисунке, то

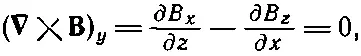
или

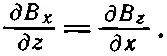(29.3)

Поскольку мы предполагаем, что ∂ B z /∂ x отрицательно, то равным ему и отрицательным должно быть и ∂ B х /∂ z. Если «номинальной» плоскостью орбиты является плоскость симметрии, где В х =0, то радиальная компонента В х будет отрицательной над плоскостью и положительной под ней. При этом линии должны быть искривлены так, как это изображено на рисунке.

Такое поле должно обладать вертикально фокусирующими свойствами. Представьте себе протон, летящий более или менее параллельно центральной орбите, но выше нее. Горизонтальная компонента Вбудет действовать на протон с силой, направленной вниз. Если же протон находится ниже центральной орбиты, то сила изменит свое направление. Таким образом, возникает эффективная «восстанавливающая сила», направленная к центру орбиты. Из наших рассуждений получается, что при условии уменьшения вертикального поля с увеличением радиуса должна происходить вертикальная фокусировка. Однако если градиент поля положительный, то происходит «вертикальная дефокусировка». Таким образом, для вертикальной фокусировки индекс поля n должен быть меньше нуля. Выше мы нашли, что для радиальной фокусировки значение n должно быть больше -1. Комбинация этих двух условий требует для удержания частиц на стабильных орбитах, чтобы

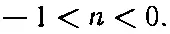
В циклотронах обычно используется величина n, приблизительно равная нулю, а в бетатронах и синхротронах типичной величиной является n=-0,6.

Столь малые величины n дают довольно «слабую» фокусировку. Ясно, что гораздо большую радиальную фокусировку можно было бы получить для большого положительного градиента ( n ≫1), но при этом вертикальные силы будут сильно дефокусирующими. Подобным же образом большой отрицательный наклон (n≪-1) давал бы большие вертикальные силы, но при этом вызывал бы сильную радиальную дефокусировку. Однако примерно 10 лет назад было установлено, что чередующееся действие областей с сильной фокусировкой и область с сильной дефокусировкой в целом приводят к фокусирующему эффекту.

Чтобы объяснить, как работает такая фокусировка , разберем сначала действие квадрупольной линзы, которая устроена по тому же принципу. Представьте себе, что к магнитному полю, изображенному на фиг. 29.12, добавлено однородное отрицательное магнитное поле, сила которого подобрана так, чтобы поле на орбите было равно нулю. Результирующее поле при малых смещениях от нейтральной точки будет напоминать изображенное на фиг. 29.13.

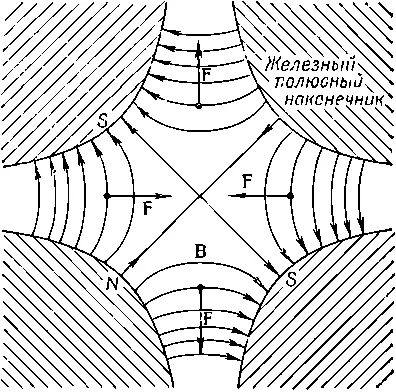
Фиг. 29.13. Горизонтально фокусирующая квадрупольная линза.

Такой четырехполюсный магнит называется «квадрупольной линзой». Положительная частица, которая входит (со стороны читателя) справа или слева от центра, снова втягивается в центр. Если же частица входит сверху или снизу от центра, то она выталкивается из него. Это горизонтально-фокусирующая линза. Если теперь обратить горизонтальный градиент, что может быть сделано переменой всех полюсов на противоположные, то знак всех сил изменится на обратный и мы получим вертикально-фокусирующую линзу (фиг. 29.14).

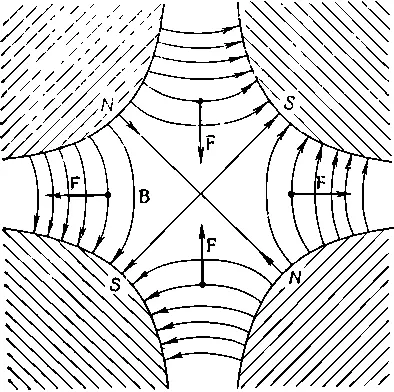
Фиг. 29.14. Вертикально-фокусирующая квадрупольная линза.

Напряженность поля у таких линз, а следовательно, и фокусирующая сила возрастают линейно с удалением от оси линзы.

Представьте себе теперь, что мы поставили подряд две такие линзы. Если частица входит с некоторым горизонтальным смещением относительно оси (фиг. 29.15, а ), то она отклонится по направлению к оси первой линзы.

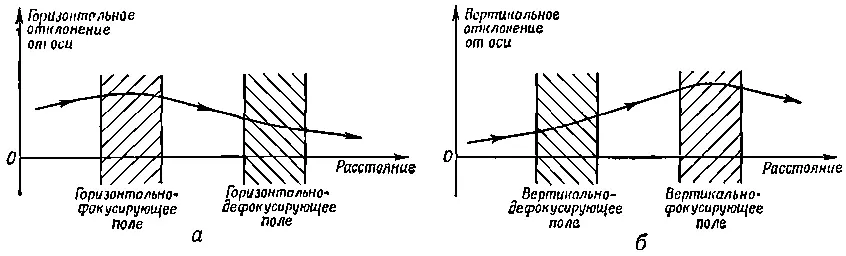
Фиг. 29.15. Горизонтальная и вертикальная фокусировка парой квадрупольных линз.

Когда же она подходит ко второй линзе, то оказывается ближе к оси, где выталкивающая сила меньше, поэтому меньшим будет и отклонение от оси. В результате же получится наклон к оси, т. е. в среднем их действие окажется горизонтально-фокусирующим. С другой стороны, если мы возьмем частицу, которая отклоняется от оси в вертикальном направлении, то путь ее будет таким, как показано на фиг. 29.15, б . Частица сначала отклоняется от оси, а затем входит во вторую линзу с большим смещением, испытывая действие большей силы, в результате чего отклоняется к оси. В целом эффект снова будет фокусирующим. Таким образом, действие пары квадрупольных линз, действующих независимо в горизонтальном и вертикальном направлениях, очень напоминает действие оптической линзы. Квадрупольные линзы используются для формирования пучка частиц и контроля над ним в точности так же, как оптические линзы используются для светового пучка.