Ричард Фейнман - Том 2. Электромагнетизм и материя

Предполагаемый эффект выстраивания мы учитывали добавлением в выражение для энергии подходящего слагаемого, приговаривая, что если соседние электронные магнитики дают среднюю намагниченность М , то магнитный момент электрона имеет сильную тенденцию смотреть в том же самом направлении, что и средняя намагниченность соседних атомов. Таким образом, для двух возможных ориентации спинов можно написать [51] Вместо В мы записали это уравнение через H=B-M/ε 0 c 2 , чтобы согласовать со сказанным в предыдущей главе. Если вам больше нравится, можете написать U=±|μ|B a =±|μ|(В+λ'M/ε 0 с 2 ), где λ'=λ-1. Это одно и то же. :

(37.1)

Когда стало ясно, что квантовая механика может объяснить нам огромные спин-ориентирующие силы, пусть даже с очевидно неправильным знаком, то было предложено, что ферромагнетизм возникает именно за счет этих сил, но что вследствие сложности железа и большого числа участвующих в игре электронов знак энергии электронов получается обратным. Как только это стало ясно, т. е. примерно с 1927 г., когда была понята квантовая механика, многие исследователи стали делать разные оценки, прикидки, полуподсчеты, стремясь получить теоретически величину λ. Но все равно наиболее поздние вычисления энергии взаимодействия между двумя электронными спинами в железе, предполагавшие прямое взаимодействие между двумя электронами в соседних атомах, дали неправильный знак . Сейчас, описывая это явление, говорят, что за все как-то ответственна сложность ситуации и что есть надежда, что кому-то, кто сумеет проделать вычисления для более сложного случая, удастся получить правильный ответ!

Полагают, что направленный вверх спин одного из электронов внутренней оболочки, который ответствен за магнетизм, стремится заставить спины электронов проводимости, витающих вокруг него, повернуться в противоположную сторону. Можно надеяться, что это ему вполне удастся, ибо электроны проводимости движутся в той же самой области, что и «магнитные» электроны. А поскольку они движутся то туда, то сюда, то могут передать свой приказ перевернуться «вверх ногами» спинам электронов других атомов; таким образом, «магнитный» электрон заставляет электрон проводимости направить спин в противоположную сторону, а тот в свою очередь заставляет следующий «магнитный» электрон направить свой спин противоположно его спину. Это двойное взаимодействие эквивалентно взаимодействию, стремящемуся выстроить два «магнитных» электрона в одном направлении. Иными словами, тенденция соседних спинов быть параллельными есть результат действия промежуточной среды, которая в некотором смысле стремится быть противоположной им обоим. Этот механизм не требует, чтобы все электроны проводимости были повернуты «вверх ногами». Достаточно, чтобы они лишь слегка стремились повернуться вниз, и шансы «магнитных» электронов повернуться вверх перевесят. Как полагают те исследователи, которые работали с этими вещами, это и есть тот механизм, который ответствен за ферромагнетизм. Но должен отметить, что вплоть до сегодняшнего дня никто не может вычислить величину λ материала, зная просто, что в периодической системе элементов этот материал стоит, скажем, под номером 26. Короче говоря, мы все еще не можем понять явление до конца.

Теперь же продолжим рассуждения о нашей теории, а потом вернемся снова назад и обсудим некоторые ошибки избранного нами пути. Если магнитный момент какого-то электрона направлен вверх, то его энергия частично обусловлена внешним полем, а частично связана с тенденцией спинов быть параллельными. Поскольку при параллельных спинах энергия меньше, то эффект получается таким же, как и от «внешнего эффективного поля». Но помните, что обязано это не истинным магнитным силам, а более сложному взаимодействию. Во всяком случае, в качестве выражений для энергии двух спиновых состояний «магнитного» электрона мы примем уравнения (37.1). Относительная вероятность этих двух состояний при температуре Т пропорциональна exp[-энергия/kT], что можно записать как е ± х , где х =|μ|(H+λM/ε 0с 2)/kT. Если затем мы вычислим среднюю величину магнитного момента, то найдем (как и в предыдущей главе), что она равна

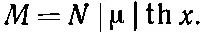(37.2)

Теперь я могу подсчитать внутреннюю энергию материала. Отметим, что энергия электрона в точности пропорциональна магнитному моменту, так что все равно, вычислять ли средний момент или среднюю энергию. Среднее значение энергии будет при этом

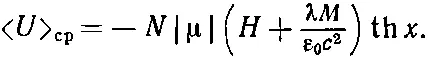
Но это не совсем верно. Выражение λM/ε 0c 2представляет взаимодействие всех возможных пар атомов, а мы должны помнить, что каждую пару следует учитывать только один раз . (Когда мы учитываем энергию одного электрона в поле остальных, а затем энергию второго электрона в поле остальных, то мы еще раз учитываем часть первой энергии.) Поэтому выражение взаимодействия мы должны разделить на 2 и наша формула для энергии приобретет вид

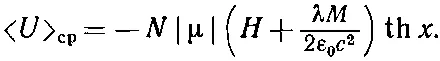(37.3)

В предыдущей главе мы обнаружили одну очень интересную особенность: для каждого материала ниже определенной температуры существует такое решение уравнений, при котором магнитный момент не равен нулю даже в отсутствие внешнего намагничивающего поля. Если в уравнении (37.2) мы положим Н =0, то найдем

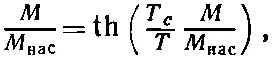(37.4)

где М нас=N|μ| и T c =|μ|λM нас / k ε 0 c 2. Решив это уравнение (графически или каким-то другим способом), мы найдем, что отношение М / М нас как функция от T / T c представляет кривую, названную на фиг. 37.1 «квантовая теория».

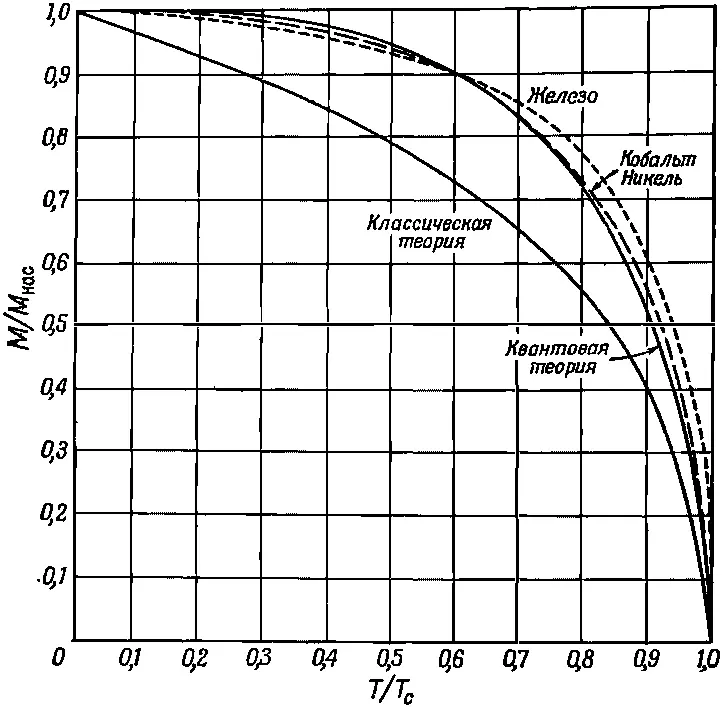
Фиг. 37.1. Зависимость спонтанной намагниченности (Н=0) ферромагнитных кристаллов от температуры.

Пунктирная кривая «Кобальт, Никель» — это полученная экспериментально кривая для кристаллов этих элементов. Теория и эксперимент находятся в разумном согласии. Там же представлены результаты классической теории, в которой вычисления проводились в предположении, что атомные магнитики могут иметь всевозможные ориентации в пространстве.