Ричард Фейнман - Том 2. Электромагнетизм и материя

похожая на формулу (11.25). Но это будет неправильно. Однако мы все же можем использовать полученные там результаты, если тщательно сравним уравнения из гл. 11 с уравнениями ферромагнетизма, которые мы напишем сейчас. Сопоставим сначала соответствующие исходные уравнения. Для областей, в которых токи проводимости и заряды отсутствуют, мы имеем:

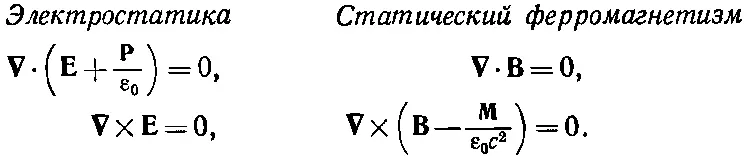(36.30)

Эти два набора уравнений можно считать аналогичными, если мы чисто математически сопоставим

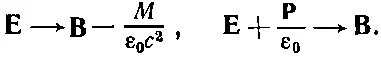
Это то же самое, что и

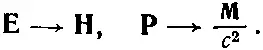(36.31)

Другими словами, если уравнения ферромагнетизма записать как

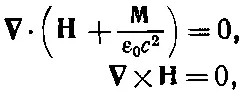(36.32)

то они будут похожи на уравнения электростатики.

В прошлом это чисто алгебраическое соответствие доставило нам некоторые неприятности. Многие начинали думать, что именно Ни есть магнитное поле. Но, как мы уже убедились, физически фундаментальными полями являются Еи В, а поле Н— понятие производное. Таким образом, хотя уравнения и аналогичны, физика их совершенно различна. Однако это не может заставить нас отказаться от принципа, что одинаковые уравнения имеют одинаковые решения.

Теперь можно воспользоваться нашими предыдущими результатами о полях внутри полости различной формы в диэлектриках, которые приведены на фиг. 36.1, для нахождения поля Н. Зная Н, можно определить и В. Например, поле Нвнутри иглообразной полости, параллельной М(согласно результату, приведенному в § 1), будет тем же самым, что и поле Нвнутри материала:

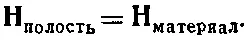
Но поскольку в нашей полости Мравна нулю, то мы получаем

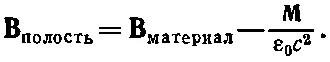(36.33)

С другой стороны, для дискообразной полости, перпендикулярной М,

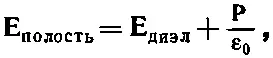
что в нашем случае превращается в

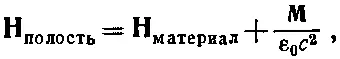
или в величинах В:

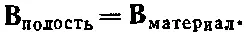(36.34)

Наконец, для сферической полости аналогия с уравнением (36.3) дала бы

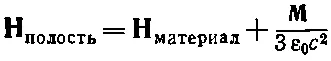
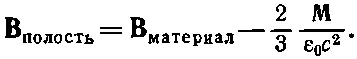(36.35)

Результаты для магнитного поля, как видите, отличаются от тех, которые мы имели для электрического поля.

Конечно, их можно получить и более физически, непосредственно используя уравнения Максвелла. Например, уравнение (36.34) непосредственно следует из уравнения ∇· B=0. (Возьмите гауссову поверхность, которая наполовину находится в материале, а наполовину — вне его.) Подобным же образом вы можете получить уравнение (36.33), воспользовавшись контурным интегралом по пути, который туда идет по полости, а назад возвращается через материал. Физически поле в полости уменьшается благодаря поверхностным токам, определяемым как ∇× М. На вашу долю остается показать, что уравнение (36.35) можно получить, рассматривая эффекты поверхностных токов на границе сферической полости.

При нахождении равновесной намагниченности из уравнения (36.29) удобнее, оказывается, иметь дело с Н, поэтому мы пишем

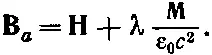(36.36)

В приближении сферической полости коэффициент λ следует взять равным 1/ 3, но, как вы увидите позже, нам придется пользоваться несколько другим его значением, а пока оставим его как подгоночный параметр. Кроме того, все поля мы возьмем в одном и том же направлении, чтобы нам не нужно было заботиться о направлении векторов. Если бы теперь мы подставили уравнение (36.36) в (36.29), то получили бы уравнение, которое связывает намагниченность М с намагничивающим полем Н :

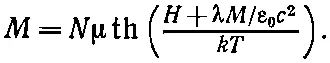
Однако это уравнение невозможно решить точно, так что мы будем делать это графически.

Сформулируем задачу в более общей форме, записывая уравнение (36.29) в виде

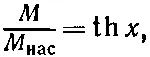(36.37)

где М нас— намагниченность насыщения, т. е. N μ, а x — величина μ B a / kT . Зависимость М / М нас от х показана на фиг. 36.13 (кривая а).

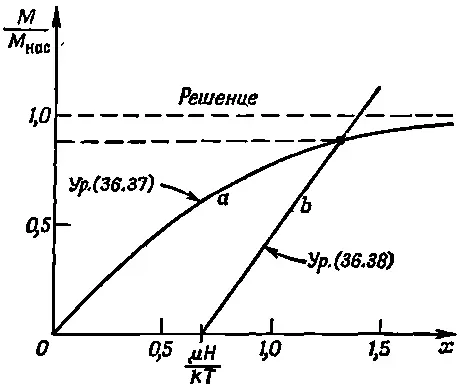
Фиг. 36.13. Графическое решение уравнений (36.37) и (36.38),

Воспользовавшись еще уравнением (36.36) для В а , можно записать х как функцию от М :

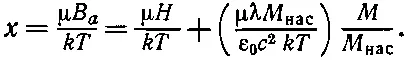(36.38)

Эта формула определяет линейную зависимость между М / М нас и х при любой величине Н . Прямая пересекается с осью х в точке x =μ H / kT , и наклон ее равен ε 0 с 2 kT /μλ М нас . Для любого частного значения Н это будет прямая, подобная прямой b на фиг. 36.13. Пересечение кривых а и о дает нам решение для М / М нас. Итак, задача решена.

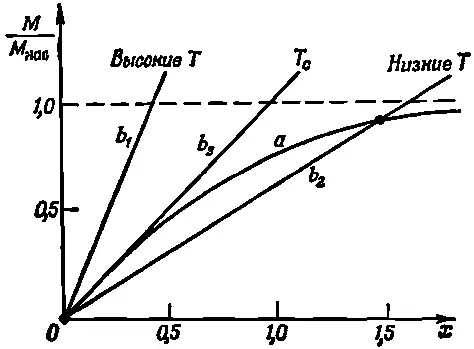
Посмотрим теперь, годны ли эти решения при различных обстоятельствах. Начнем с H =0. Здесь представляются две возможности, показанные кривыми b 1и b 2на фиг. 36.14.