Ричард Фейнман - Том 2. Электромагнетизм и материя

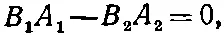
а поскольку А 1= А 2, то отсюда следует, что В 1= В 2.

Посмотрим теперь на Н . Мы снова можем воспользоваться уравнением (36.19), взяв криволинейный интеграл по контуру Г (см. фиг. 36.11,б). Как и прежде, правая часть равна NI — произведению числа витков на ток. Однако теперь Н в железе и в воздухе будет различным. Обозначая через Н 2поле в железе, а через l 2— длину пути по окружности ярма, мы видим, что эта часть кривой дает вклад в интеграл H 2 l 2. Если же поле в зазоре равно Н 1, а ширина его l 1, то вклад зазора оказывается равным H 1 l 1. Таким образом, получаем

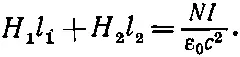(36.26)

Но это еще не все. Нам известно еще, что намагниченность в воздушной щели пренебрежимо мала, так что B 1= H 1. А так как B 1=B 2, то уравнение (36.26) принимает вид

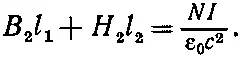(36.27)

Остаются еще два неизвестных. Чтобы найти В 2и H 2, необходимо еще одно соотношение, которое связывает В с H в железе.

Если можно приближенно считать, что B 2=μ H 2, то уравнение разрешается алгебраически. Рассмотрим более общий случай, для которого кривая намагничивания железа имеет вид, изображенный на фиг. 36.8. Единственное, что нам нужно, — это найти совместное решение этого функционального соотношения с уравнением (36.27). Его можно найти, строя зависимость (36.27) на одном графике с кривой намагничивания, как это сделано на фиг. 36.12. Точки, где эти кривые пересекутся, и будут нашими решениями.

Для данного тока I уравнение (36.27) описывается прямой линией, обозначенной I >0 на фиг. 36.12. Эта линия пересекает ось Н ( B 2=0) в точке H 2= NI /ε 0 c 2 l 2и имеет наклон - l 2/ l 1Различные величины токов приводят просто к горизонтальному сдвигу этой линии. Из фиг. 36.12 мы видим, что при данном токе существует несколько различных решений, зависящих от того, каким образом вы получили их.

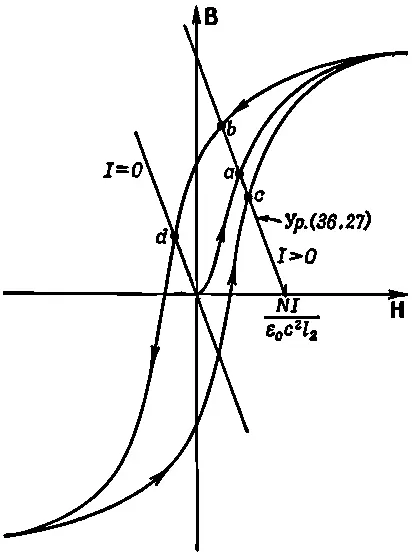
Фиг. 36.12. Определение поля в электромагните.

Если вы только что построили магнит и включили ток I , то поле B 2(которое равно B 1) будет иметь величину, определяемую точкой а . Если вы сначала увеличили ток до очень большой величины, а затем понизили до I , то значение поля будет определяться точкой b . А если, увеличивая ток от большого отрицательного значения, вы дошли до I , то поле определяется точкой с . Поле в зазоре зависит от того, как вы поступали в прошлом.

Если ток в магните равен нулю, то соотношение между В 2и H 2в уравнении (36.27) изображается кривой, обозначенной I =0 на фиг. 36.12. Здесь опять возможны различные решения. Если вы первоначально «насытили» железо, то в магните может сохраниться значительное остаточное поле, определяемое точкой d . Вы можете снять обмотку и получить постоянный магнит. Нетрудно понять, что для хорошего постоянного магнита необходим материал с широкой петлей гистерезиса. Такую очень широкую петлю имеют специальные сплавы, подобные Алнико V.

Обратимся теперь к вопросу, почему в ферромагнитных материалах даже малые магнитные поля приводят к такой большой намагниченности. Намагниченность ферромагнитных материалов типа железа или никеля образуется благодаря магнитным моментам электронов одной из внутренних оболочек атома. Магнитный момент μкаждого электрона равен произведению q /2 m на g-фактор и момент количества движения J. Для отдельного электрона при отсутствии чисто орбитального движения g=2, а компонента Jв любом направлении, скажем, в направлении оси z , равна ± ℏ /2, так что компонента μв направлении оси z будет

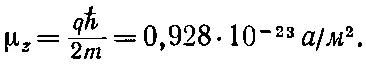(36.28)

В атоме железа вклад в ферромагнетизм фактически дают только два электрона, так что для упрощения рассуждений мы будем говорить об атоме никеля, который является ферромагнетиком, подобно железу, но имеет на той же внутренней оболочке только один «ферромагнитный» электрон. (Все рассуждения нетрудно затем распространить и на железо.)

Все дело в том, что точно так же, как и в описанных нами парамагнитных материалах, атомные магнитики в присутствии внешнего магнитного поля Встремятся выстроиться по полю, но их сбивает тепловое движение. В предыдущей главе мы выяснили, что равновесие между силами магнитного поля, старающимися выстроить атомные магнитики, и действием теплового движения, стремящегося их сбить, приводит к тому, что средний магнитный момент единицы объема в направлении Воказывается равным

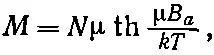(36.29)

где под В а мы подразумеваем поле, действующее на атом, а под kT — тепловую (больцмановскую) энергию. В теории парамагнетизма мы в качестве В а использовали само поле В, пренебрегая при этом частью поля, действующего на каждый атом со стороны соседнего. Но в случае ферромагнетиков возникает усложнение. Мы уже не можем в качестве поля В а , действующего на индивидуальный атом, брать среднее поле в железе. Вместо этого нам следует поступить так же, как это делалось в случае диэлектрика: нам нужно найти локальное поле, действующее на отдельный атом. При точном решении нам следовало бы сложить вклады всех полей от других атомов кристаллической решетки, действующих на рассматриваемый нами атом. Но подобно тому как мы поступали в случае диэлектрика, сделаем приближение, состоящее в том, что поле, действующее на атом, будет таким же, как и в маленькой сферической полости внутри материала (предполагая при этом, как и раньше, что моменты соседних атомов не изменяются из-за наличия полости).

Следуя рассуждениям гл. 11 (вып. 5), мы можем надеяться, что должна получиться формула