Ричард Фейнман - Том 2. Электромагнетизм и материя
- Название:Том 2. Электромагнетизм и материя
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 2. Электромагнетизм и материя краткое содержание
Том 2. Электромагнетизм и материя - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Чтобы проверить это представление или, лучше сказать, чтобы выяснить, к каким следствиям оно приведет, мы сперва рассмотрим разницу в энергиях основных состояний обоих ядер. Чтобы модель была совсем простой, положим, что ядра — это шары радиуса r (который нужно определить), содержащие Z протонов. Если считать ядро шаром с равномерно распределенным зарядом, то можно ожидать, что электростатическая энергия [из уравнения (8.7)] окажется равной
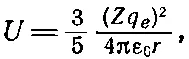 (8.22)
(8.22)
где q e — элементарный заряд протона. Из-за того, что Z равно для В 11пяти, а для С 11шести, электростатические энергии будут различаться.
Но при таком малом количестве протонов уравнение (8.22) не совсем правильно. Если мы подсчитаем электрическую энергию взаимодействия всех пар протонов, рассматриваемых как точки, примерно однородно распределенные по шару, то увидим, что величину Z 2в (8.22) придется заменить на Z ( Z -1), так что энергия будет равна
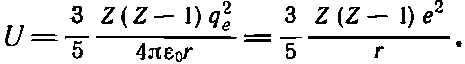 (8.23)
(8.23)
Если известен радиус ядра r, мы можем воспользоваться выражением (8.23), чтобы определить разницу электростатических энергий ядер В 11и С 11. Но проделаем обратное: из наблюдаемой разницы в энергиях вычислим радиус, считая, что вся существующая разница по происхождению — электростатическая.
В общем это не совсем верно. Разность энергий 1,982 Мэв двух основных состояний В 11и С 11включает энергии покоя, т. е. энергии mc 2всех частиц. Переходя от В 11к С 11, мы замещаем нейтрон протоном, масса которого чуть поменьше. Так что часть разности энергий — это разница в массах покоя нейтрона и протона, составляющая 0,784 Мэв . Та разность, которую надо сравнивать с электростатической энергией, тем самым больше 1,982 Мэв ; она равна
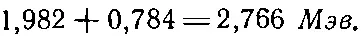
Подставив эту энергию в (8.23), для радиуса В 11или С 11получим
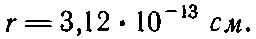 (8.24)
(8.24)
Имеет ли это число какой-нибудь смысл? Чтобы это проверить, сравним его с другими определениями радиусов этих ядер. Например, можно определить радиус ядра иначе, наблюдая, как рассеивает оно быстрые частицы. В ходе этих измерений выяснилось, что плотность вещества во всех ядрах примерно одинакова, т. е. их объемы пропорциональны числу содержащихся в них частиц. Если через А обозначить число протонов и нейтронов в ядре (число, очень близко пропорциональное его массе), то оказывается, что радиус ядра дается выражением
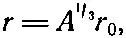 (8.25)
(8.25)
где
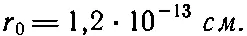 (8.26)
(8.26)
Из этих измерений мы получим, что радиус ядра В 11(или С 11)должен быть примерно равен
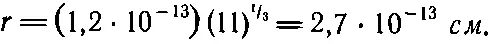
Сравнив это с выражением (8.24), мы увидим, что наши предположения об электростатическом происхождении разницы в энергиях В 11и С 11не столь неверны; расхождение едва ли достигает 15% (а это не так уж скверно для первого расчета по теории ядра!).
Причина расхождения, по всей вероятности, состоит в следующем. Согласно нашему нынешнему пониманию ядер, четное количество ядерных частиц (в случае В 11пять нейтронов с пятью протонами) образует своего рода оболочку ; когда к этой оболочке добавляется еще одна частица, то вместо того, чтобы поглотиться, она начинает обращаться вокруг оболочки. Если это так, то для добавочного протона нужно взять другое значение электростатической энергии. Нужно считать, что избыток энергии С 11над В 11как раз равен
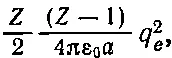
т. е. равен энергии, необходимой для того, чтобы снаружи оболочки появился еще один протон. Это число составляет 5/ 6величины, предсказываемой уравнением (8.23), так что новое значение радиуса будет равно 5/ 6от (8.24). Оно намного лучше согласуется с прямыми измерениями.
Согласие в цифрах приводит к двум выводам. Первый : законы электричества, видимо, действуют и на столь малых расстояниях, как 10 -13 см. Второй : мы убедились в замечательном совпадении — неэлектрическая часть сил взаимодействия протона с протоном, нейтрона с нейтроном и протона с нейтроном одинакова.
§ 5. Энергия в электростатическом поле
Рассмотрим теперь другие способы подсчета электростатической энергии. Все они могут быть получены из основного соотношения (8.3) суммированием (по всем парам) взаимных энергий каждой пары зарядов. Прежде всего мы хотим написать выражение для энергии распределения зарядов. Как обычно, считаем, что каждый элемент объема dV содержит в себе элемент заряда ρ dV . Тогда уравнение (8.3) запишется так:
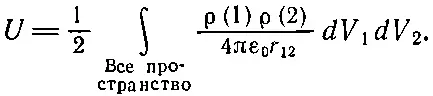 (8.27)
(8.27)
Обратите внимание на появление множителя 1/ 2. Он возник из-за того, что в двойном интеграле по dV 1и по dV 2каждая пара элементов заряда считалась дважды. (Не существует удобной записи интеграла, в которой каждая пара считалась бы только по одному разу.) Затем заметьте, что интеграл по dV 2в (8.27) — это просто потенциал в точке (1), т. е.
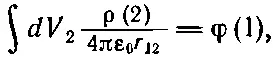
так что (8.27) можно записать в виде
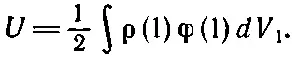
А так как точка (2) при этом выпала, то можно написать просто
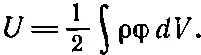 (8.28)
(8.28)
Это уравнение можно истолковать так. Потенциальная энергия заряда ρ dV равна произведению этого заряда на потенциал в той же точке. Вся энергия поэтому равна интегралу от φρdV. Но, кроме этого, есть множитель 1/ 2. Он все еще необходим, потому что энергии считаются дважды. Взаимная энергия двух зарядов равна заряду одного из них на потенциал другого в этой точке. Или заряду другого на потенциал от первого во второй точке. Так что для двух точечных зарядов можно написать
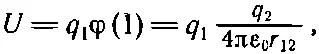
Интервал:
Закладка:






