Ричард Фейнман - Том 2. Электромагнетизм и материя

Фиг. 8.3. Чему равен вращательный момент, действующий на переменный конденсатор?

Вернемся к частному случаю плоского конденсатора; мы можем взять формулу для емкости, выведенную в гл. 6:

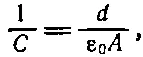(8.16)

где А —площадь каждой обкладки. Если промежуток увеличится на Δz, то

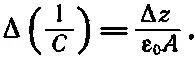
Из (8.14) тогда следует, что сила притяжения между двумя обкладками равна

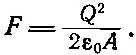(8.17)

Взглянем на уравнение (8.17) повнимательнее и подумаем, нельзя ли сказать, как возникает эта сила. Если заряд на одной из обкладок мы запишем в виде

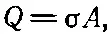
то (8.17) можно будет переписать так:

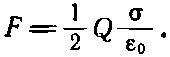
Или поскольку поле между пластинами равно

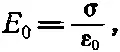
то

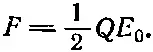(8.18)

Можно было сразу догадаться, что сила, действующая на одну из пластин, будет равна заряду Q этой пластины, умноженному на поле, действующее на заряд. Но что удивляет, так это множитель 1/ 2. Дело в том, что Е 0—это не то поле, которое действует на заряды. Если вообразить, что заряд на поверхности пластины занимает какой-то тонкий слой (фиг. 8.4), то поле будет меняться от нуля на внутренней границе слоя до Е 0в пространстве снаружи пластин. Среднее поле, действующее на поверхностные заряды, равно Е 0/2. Вот отчего в (8.18) стоит множитель 1/ 2.

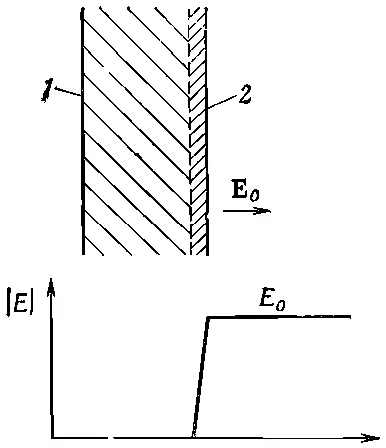
Фиг. 8.4. Поле у поверхности проводника меняется от нуля до E 0 =σ/ε 0 , когда пересечен слой поверхностного заряда. 1 — проводящая пластина; 2 — слой поверхностного заряда.

Вы должны обратить внимание на то, что, рассчитывая виртуальную работу, мы предположили, что заряд конденсатора постоянен, что конденсатор не был электрически связан с другими предметами и полный заряд не мог изменяться.

А теперь пусть мы предположили, что при виртуальных перемещениях конденсатор поддерживается при постоянной разности потенциалов. Тогда мы должны были бы взять

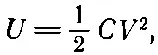
и вместо (8.15) мы бы имели

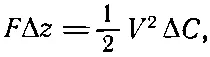
что приводит к силе, равной по величине той, что была получена в уравнении (8.15) (так как V = Q / C ), но с противоположным знаком!

Конечно, сила, действующая между пластинами конденсатора, не меняет свой знак, когда мы отсоединяем конденсатор от источника электричества. Кроме того, мы знаем, что две пластины с разноименными электрическими зарядами должны притягиваться. Принцип виртуальной работы во втором случае был применен неправильно, мы не приняли во внимание виртуальную работу, производимую источником, заряжающим конденсатор. Это значит, что для того, чтобы удержать потенциал при постоянном значении V , когда меняется емкость, источник электричества должен снабдить конденсатор зарядом VΔC. Но этот заряд поступает при потенциале V, так что работа, выполняемая электрической системой, удерживающей заряд постоянным, равна V 2ΔC. Механическая работа FΔz плюс эта электрическая работа V 2ΔC вместе приводят к изменению полной энергии конденсатора на 1/ 2V 2ΔC. Поэтому на механическую работу, как и прежде, приходится F Δ z =- 1/ 2V 2ΔC.

Рассмотрим теперь применение понятия электростатической энергии в атомной физике. Мы не можем запросто измерять силы, действующие между атомами, но часто нас интересует разница в энергиях двух расстановок атомов (к примеру, энергия химических изменений). Так как атомные силы в основе своей — это силы электрические, то и химическая энергия в главной своей части — это просто электростатическая энергия.

Рассмотрим, например, электростатическую энергию ионной решетки. Ионный кристалл, такой, как NaCl, состоит из положительных и отрицательных ионов, которые можно считать жесткими сферами. Они электрически притягиваются, пока не соприкоснутся; затем вступает в дело сила отталкивания, которая быстро возрастает, если мы попытаемся сблизить их теснее.

Для первоначального приближения вообразим себе совокупность жестких сфер, представляющих атомы в кристалле соли. Строение такой решетки было определено с помощью дифракции рентгеновских лучей. Эта решетка кубическая — что-то вроде трехмерной шахматной доски. Сечение ее изображено на фиг. 8.5. Промежуток между ионами 2,81 Å (или 2,81·10 -8 см ).

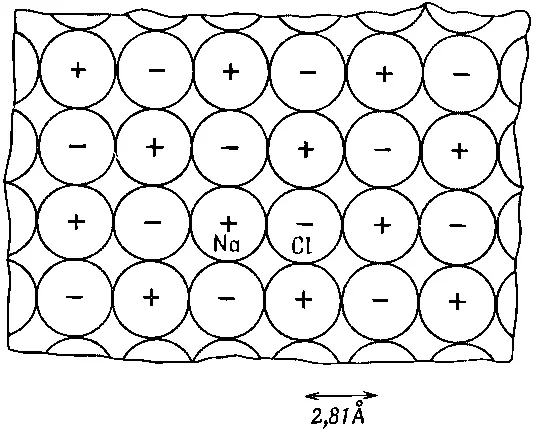
Фиг. 8.5. Поперечный разрез кристалла соли в масштабе нескольких атомов. В двух перпендикулярных к плоскости рисунка сечениях будет такое же шахматное расположение ионов Na и Сl (см. вып. 1, фиг. 1.7).

Если наше представление о системе правильно, мы должны уметь проверить его, задав следующий вопрос: сколько понадобится энергии, чтобы разбросать эти ионы, т. е. полностью разделить кристалл на ионы? Эта энергия должна быть равна теплоте испарения соли плюс энергия, требуемая для диссоциации молекул на ионы. Полная энергия разделения NaCl на ионы, как следует из опыта, равна 7,92 эв на молекулу.

Пользуясь коэффициентом перевода

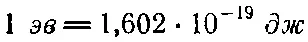
и числом Авогадро (количество молекул в грамм-молекуле)

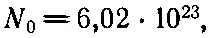
можно представить энергию испарения в виде

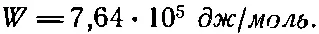
Излюбленная единица энергии, которой пользуются физико-химики,— килокалория, равная 4190 дж ; так что 1 эв на молекулу — это все равно что 23 ккал / моль . Химик сказал бы поэтому, что энергия диссоциации NaCl равна